题目内容
【题目】已知
的三边长分别为a，b，c，其面积为S，则的内切圆O的半径
.这是一道平面几何题，其证明方法采用“等面积法”设空间四面体
四个面的面积分别为积为V，内切球半径为R.请用类比推理方法猜测对空间四面体存在类似结论为______.
【答案】
【解析】
根据平面与空间之间的类比推理，由点类比点或直线，由直线类比直线或平面，由内切圆类比内切球，由平面图形面积类比立体图形的体积，结合求三角形的面积的方法类比求四面体的体积即可.
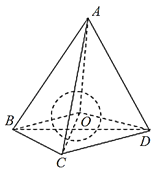
解：设四面体的内切球的球心为O，则球心O到四个面的距离都是R，
所以四面体的体积等于以O为顶点，分别以四个面为底面的4个三棱锥体积的和.
则四面体的体积为 
猜想：四面体ABCD的各表面面积分别为S1，S2，S3，S4，其体积为V，
则四面体ABCD的内切球半径.
故答案为：.
练习册系列答案
相关题目
