题目内容
【题目】在等比数列![]() 中,
中,
(1)已知![]() ,求
,求![]() 和
和![]() ;
;
(2)已知![]() ,求
,求![]() 和
和![]() ;
;
(3)已知![]() ,
,![]() ,求
,求![]() 和
和![]() ;
;
(4)已知![]() ,
,![]() ,求
,求![]() .
.
【答案】(1)![]() ,
,![]() ;
;
(2)![]() ,
,![]() ;
;
(3)![]() ,
,![]() 或
或![]() ,
, ;
;
(4)![]() .
.
【解析】
设等比数列![]() 的公比为
的公比为![]() .
.
(1)确定出等比数列![]() 的首项和公比,利用等比数列的前
的首项和公比,利用等比数列的前![]() 项和公式求出
项和公式求出![]() ,并求出
,并求出![]() ;
;
(2)利用![]() 求出
求出![]() ,再令
,再令![]() ,得出
,得出![]() ,再检验
,再检验![]() 是否满足
是否满足![]() ,由此可得出数列
,由此可得出数列![]() 的通项公式,并求出
的通项公式,并求出![]() 的值;
的值;
(3)利用首项和公比建立方程组,求出这两个量,然后利用等比数列的通项公式和前![]() 项和公式求出
项和公式求出![]() 和
和![]() ;
;
(4)分![]() 和
和![]() 两种情况,建立
两种情况,建立![]() 和
和![]() 的方程组,解出这两个量,然后利用等比数列的前
的方程组,解出这两个量,然后利用等比数列的前![]() 项和公式可求出
项和公式可求出![]() 的值.
的值.
设等比数列![]() 的公比为
的公比为![]() .
.
(1)![]() ,所以,数列
,所以,数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列,
为公比的等比数列,
因此, ,
,![]() ;
;
(2)当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
![]() 适合上式,所以,对任意的
适合上式,所以,对任意的![]() ,
,![]() ,因此,
,因此,![]() ;
;
(3)由 ,得
,得 ,解得
,解得![]() 或
或 .
.
当![]() 时,
时,![]() ,
,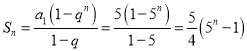 ;
;
当![]() ,
,![]() 时,
时,![]() ,
,
 ;
;
(4)当![]() 时,
时,![]() ,得
,得![]() ,
,
此时,![]() ,矛盾;
,矛盾;
当![]() 时,
时, ,
,
所以, ,解得
,解得 ,
,
因此, .
.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
【题目】某大型水果超市每天以![]() 元/千克的价格从水果基地购进若干
元/千克的价格从水果基地购进若干![]() 水果,然后以
水果,然后以![]() 元/千克的价格出售,若有剩余,则将剩下的水果以
元/千克的价格出售,若有剩余,则将剩下的水果以![]() 元/千克的价格退回水果基地,为了确定进货数量,该超市记录了
元/千克的价格退回水果基地,为了确定进货数量,该超市记录了![]() 水果最近
水果最近![]() 天的日需求量(单位:千克),整理得下表:
天的日需求量(单位:千克),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以![]() 天记录的各日需求量的频率代替各日需求量的概率.
天记录的各日需求量的频率代替各日需求量的概率.
(1)求该超市![]() 水果日需求量
水果日需求量![]() (单位:千克)的分布列;
(单位:千克)的分布列;
(2)若该超市一天购进![]() 水果
水果![]() 千克,记超市当天
千克,记超市当天![]() 水果获得的利润为
水果获得的利润为![]() (单位:元),求
(单位:元),求![]() 的分布列及其数学期望.
的分布列及其数学期望.




