题目内容
若椭圆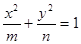 与双曲线
与双曲线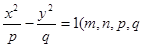 均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则
均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则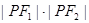 等于 ( )
等于 ( )
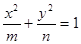 与双曲线
与双曲线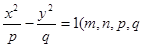 均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则
均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则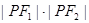 等于 ( )
等于 ( )A.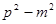 | B.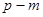 | C.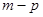 | D.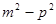 |
C
分析:设|PF1|>|PF2|,根据椭圆和双曲线的定义可分别表示出|PF1|+|PF2|和|PF1|-|PF2|,进而可表示出|PF1|和|PF2|,根据焦点相同可求得m-n=p+q,整理可得m-p=n+q,进而可求得|pF1|?|pF2|的表达式.
解:由椭圆和双曲线定义
不妨设|PF1|>|PF2|
则|PF1|+|PF2|=2
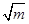
|PF1|-|PF2|=2
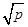
所以|PF1|=
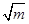 +
+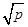
|PF2|=
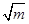 -
-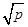
∴|pF1|?|pF2|=m-p
∵焦点相同
c2=m-n=p+q
∴m-p=n+q
所以|pF1|?|pF2|=m-p或n+q
故选C

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 抛物线
抛物线
 是C1的任意两条互相垂直的切线,并设
是C1的任意两条互相垂直的切线,并设 ,证明
,证明 :点M的纵坐标为定值;
:点M的纵坐标为定值;
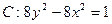 的焦点
的焦点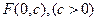 为焦点.
为焦点.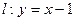 上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐标;
上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐标;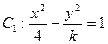 按向量
按向量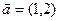 平移后得到曲线
平移后得到曲线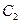 ,曲线
,曲线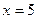 ,则
,则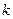 的值为____________,离心率
的值为____________,离心率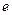 为_________.
为_________.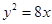 的焦点到双曲线
的焦点到双曲线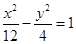 的渐近线的距离为( )
的渐近线的距离为( )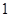
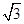
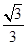
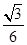
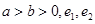 分别是圆锥曲线
分别是圆锥曲线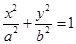 和
和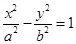 的离心率,设
的离心率,设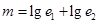 ,则
,则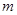 的取值范围是
的取值范围是 ,0)
,0) )
)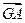 +
+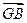 +
+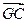 =0;②|
=0;②|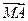 |=|
|=|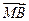 |=|
|=|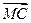 |;③
|;③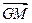 ∥
∥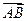 .(Ⅰ)求△ABC的顶点C的轨迹方程;(Ⅱ)是否存在过点P(3,0)的直线l与(Ⅰ)中轨迹交于E、F两点,且OE⊥OF?若存在,求出直线l斜率k的值;若不存在,说明理由.
.(Ⅰ)求△ABC的顶点C的轨迹方程;(Ⅱ)是否存在过点P(3,0)的直线l与(Ⅰ)中轨迹交于E、F两点,且OE⊥OF?若存在,求出直线l斜率k的值;若不存在,说明理由.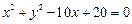 相切,过点P(-4,0)作斜率为
相切,过点P(-4,0)作斜率为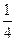 的直线l,使得l和G交于A、B两点,和y轴交于点C,并且点P在线段AB上,又满足
的直线l,使得l和G交于A、B两点,和y轴交于点C,并且点P在线段AB上,又满足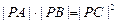
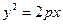
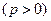 与双曲线
与双曲线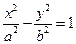
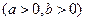 有相同的焦点
有相同的焦点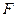 ,点
,点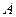 是两曲线的一个交点,且
是两曲线的一个交点,且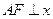 轴,若
轴,若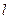 为双曲线的一条渐近线,则
为双曲线的一条渐近线,则


