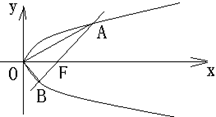
题目内容
已知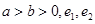 分别是圆锥曲线
分别是圆锥曲线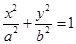 和
和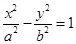 的离心率,设
的离心率,设
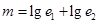 ,则
,则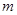 的取值范围是
的取值范围是
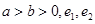 分别是圆锥曲线
分别是圆锥曲线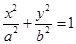 和
和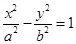 的离心率,设
的离心率,设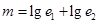 ,则
,则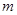 的取值范围是
的取值范围是A.( ,0) ,0) | B.(0, ) ) | C.( ,1) ,1) | D.(1, ) ) |
A
分析:先根据a>b>0推断出0<
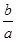 <1,进而利用椭圆和双曲线的性质分别表示出e1和e2,进而求得e1e2的表达式,求得e1e2的范围,代入m=lne1+lne2中求得m的范围.
<1,进而利用椭圆和双曲线的性质分别表示出e1和e2,进而求得e1e2的表达式,求得e1e2的范围,代入m=lne1+lne2中求得m的范围.解:由条件得:0<
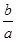 <1,e1=
<1,e1=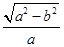 ,e2=
,e2=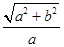 ,
,则e1?e2=
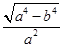 =
=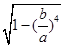
∴0<e1e2<1,
所以m=lge1+lge2=lg(e1e2)<0.
故答案为:A

练习册系列答案
相关题目
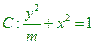 ;(1)由曲线C上任一点E向X轴作垂线,垂足为F,
;(1)由曲线C上任一点E向X轴作垂线,垂足为F,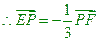 。问:点P的轨迹可能是圆吗?请说明理由;(2)如果直线L的斜率为
。问:点P的轨迹可能是圆吗?请说明理由;(2)如果直线L的斜率为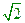 ,且过点
,且过点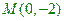 ,直线L交曲线C于A,B两点,又
,直线L交曲线C于A,B两点,又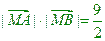 ,求曲线C的方程。
,求曲线C的方程。 
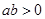 ”是“方程
”是“方程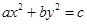 表示椭圆”的 ( )
表示椭圆”的 ( )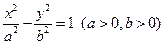 的一个焦点是
的一个焦点是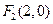 ,且
,且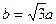 。
。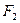 的直线
的直线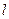 的一个法向量为
的一个法向量为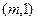 ,当直线
,当直线
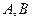 不同的两点时,求实数
不同的两点时,求实数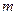 的取值范围;并证明
的取值范围;并证明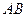 中点
中点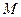 在曲线
在曲线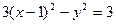 上。
上。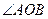 为锐角?若存在,请求出
为锐角?若存在,请求出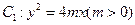 的准线与
的准线与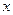 轴交于
轴交于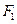 ,焦点为
,焦点为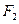 ;以
;以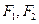 为焦点,离心率
为焦点,离心率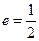 的椭圆
的椭圆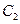 与抛物线
与抛物线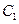 在
在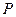 ,延长
,延长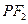 交抛物线于点
交抛物线于点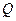 ,
,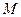 是抛物线
是抛物线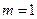 时,求椭圆
时,求椭圆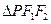 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求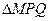 面积的最大值.
面积的最大值.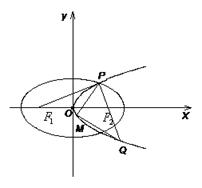
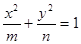 与双曲线
与双曲线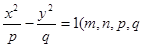 均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则
均为正数)有共同的焦点F1,F2,P是两曲线的一个公共点,则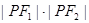 等于 ( )
等于 ( )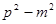
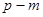
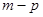
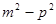
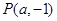 (
(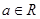 ),过点
),过点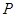 作抛物线
作抛物线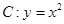 的切线,切点分别为
的切线,切点分别为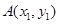 、
、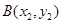 (其中
(其中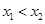 ).
).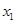 与
与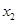 的值(用
的值(用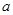 表示);
表示);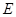 与直线
与直线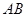 相切,求圆
相切,求圆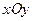 中的抛物线
中的抛物线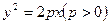 的焦点
的焦点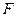 作一条倾斜角为
作一条倾斜角为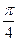 的直线与抛物线相交于A,B两点。
的直线与抛物线相交于A,B两点。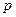 表示A,B之间的距离;
表示A,B之间的距离; 的大小是与
的大小是与