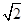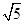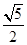题目内容
在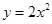 上有一点
上有一点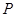 ,它到
,它到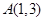 的距离与它到焦点的距离之和最小,则点
的距离与它到焦点的距离之和最小,则点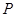 的坐标是( )
的坐标是( )
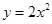 上有一点
上有一点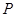 ,它到
,它到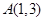 的距离与它到焦点的距离之和最小,则点
的距离与它到焦点的距离之和最小,则点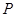 的坐标是( )
的坐标是( )| A.(-2,1) | B.(1,2) | C.(2,1) | D.(-1,2) |
B
考点:
专题:计算题.
分析:依题意可知当点P,A及抛物线焦点F在同一条直线上且A在P,F之间时P到A的距离与它到焦点的距离之和最小.题意可知点A在坐标的第一象限,则可知点P也应在第一象限,排除A,D项,把B,C项中的点分别代入抛物线方程,可知C项的点不在抛物线上,答案只能是B.
解答:解:依题意可知当点P,A及抛物线焦点F在同一条直线上且A在P,F之间时P到A的距离与它到焦点的距离之和最小
∵点A在坐标的第一象限,
∴点P也应在第一象限,排除A,D项,
又∵C项中(2,1)点不在抛物线上,
故答案只能是B
故选B
点评:本题主要考查了抛物线的应用.作为选择题,可以用数形结合的方法,对明显不符合的选项进行排除,可不用按部就班的计算出每一步骤,节省时间.
专题:计算题.
分析:依题意可知当点P,A及抛物线焦点F在同一条直线上且A在P,F之间时P到A的距离与它到焦点的距离之和最小.题意可知点A在坐标的第一象限,则可知点P也应在第一象限,排除A,D项,把B,C项中的点分别代入抛物线方程,可知C项的点不在抛物线上,答案只能是B.
解答:解:依题意可知当点P,A及抛物线焦点F在同一条直线上且A在P,F之间时P到A的距离与它到焦点的距离之和最小
∵点A在坐标的第一象限,
∴点P也应在第一象限,排除A,D项,
又∵C项中(2,1)点不在抛物线上,
故答案只能是B
故选B
点评:本题主要考查了抛物线的应用.作为选择题,可以用数形结合的方法,对明显不符合的选项进行排除,可不用按部就班的计算出每一步骤,节省时间.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
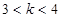 ,则二次曲线
,则二次曲线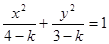 的焦点坐标是( )
的焦点坐标是( )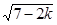 ,0)
,0) 与曲线
与曲线 有公共点,则实数
有公共点,则实数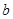 的取值范围是( ▲ )
的取值范围是( ▲ ) 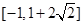
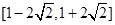
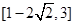
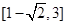
 (1,0)和定圆B:
(1,0)和定圆B: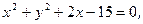 动圆P和定圆B相切并过A点,
动圆P和定圆B相切并过A点, 的最大值。
的最大值。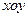 中,设点
中,设点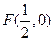 ,直线
,直线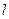 :
: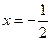 ,点
,点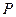 在直线
在直线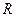 是线段
是线段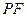 与
与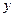 轴的交点,
轴的交点, 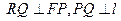 .
.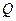 的轨迹的方程
的轨迹的方程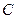 ;
;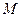 过
过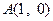 ,且圆心
,且圆心 线
线
 是圆
是圆 是否为定值?请说明理由.
是否为定值?请说明理由.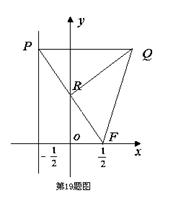
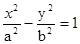 与椭圆
与椭圆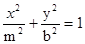 (a>0,m>b>0)的离心率互为倒数,那
(a>0,m>b>0)的离心率互为倒数,那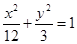 的焦点
的焦点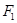 和
和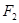 ,点P在椭圆上,如果线段
,点P在椭圆上,如果线段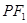 的中点在
的中点在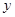 轴
轴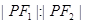 的值为( )
的值为( )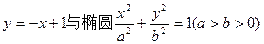 相交于A、B两点。
相交于A、B两点。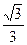 ,焦距为2,求椭圆的标准方程;
,焦距为2,求椭圆的标准方程;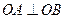 (其中O为坐标原点),当椭圆的离率
(其中O为坐标原点),当椭圆的离率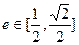 时,求椭圆的长轴长的最大值。
时,求椭圆的长轴长的最大值。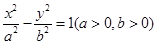 的一条渐近线方程为
的一条渐近线方程为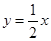 ,则该双曲线的离心率的值为
,则该双曲线的离心率的值为