题目内容
双曲线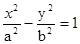 与椭圆
与椭圆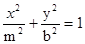 (a>0,m>b>0)的离心率互为倒数,那
(a>0,m>b>0)的离心率互为倒数,那
么以a、b、m为边长的三角形是
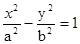 与椭圆
与椭圆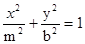 (a>0,m>b>0)的离心率互为倒数,那
(a>0,m>b>0)的离心率互为倒数,那么以a、b、m为边长的三角形是
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.等边三角形 |
C
析:求出椭圆与双曲线的离心率,利用离心率互为倒数,推出a,b,m的关系,判断三角形的形状.
解答:解:双曲线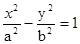 和椭圆
和椭圆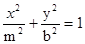 (a>0,m>b>0)的离心率互为倒数,所以
(a>0,m>b>0)的离心率互为倒数,所以
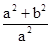 ?
?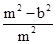 =1,
=1,
所以b2m2-a2b2-b4=0即m2=a2+b2,所以以a,b,m为边长的三角形是直角三角形.
故选C.
解答:解:双曲线
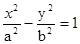 和椭圆
和椭圆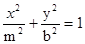 (a>0,m>b>0)的离心率互为倒数,所以
(a>0,m>b>0)的离心率互为倒数,所以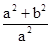 ?
?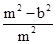 =1,
=1,所以b2m2-a2b2-b4=0即m2=a2+b2,所以以a,b,m为边长的三角形是直角三角形.
故选C.

练习册系列答案
相关题目
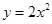 上有一点
上有一点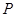 ,它到
,它到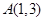 的距离与它到焦点的距离之和最小,则点
的距离与它到焦点的距离之和最小,则点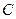 上的动点
上的动点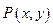 满足到点
满足到点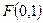 的距离比到直线
的距离比到直线 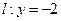 的距离小
的距离小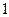 .
. 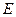 在直线
在直线 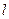 上,过点
上,过点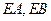 ,切点分别为
,切点分别为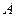 、
、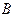 .
.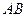 恒过一定点,并求出该定点的坐标;
恒过一定点,并求出该定点的坐标;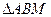 为等边三角形(
为等边三角形(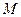 点也在直线
点也在直线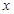
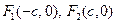 是椭圆
是椭圆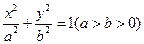 的左、右焦点,过点
的左、右焦点,过点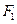 作
作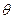 的动直线
的动直线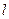 交椭圆于
交椭圆于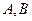 两点.当
两点.当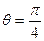 时,
时,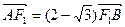 ,且
,且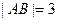 .
.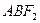 面积的最大值,并求出使面积达到最大值时直线
面积的最大值,并求出使面积达到最大值时直线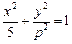 的左焦点在抛物线
的左焦点在抛物线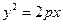 的准线上,则p的值为_______;
的准线上,则p的值为_______;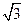 ,若它的一条准线与抛物线
,若它的一条准线与抛物线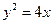 的准线重合,则该双曲线的方程是
的准线重合,则该双曲线的方程是 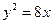 的焦点坐标是___________
的焦点坐标是___________