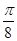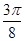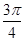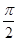题目内容
设f(x)=asinx+bcos2x,其中a,b∈R,ab≠0.若f(x)≤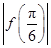 对一切x∈R恒成立,则
对一切x∈R恒成立,则
①f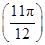 =0;
=0;
②︱f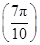 ︱<︱f
︱<︱f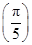 ︱;
︱;
③f(x)既不是奇函数也不是偶函数;
④f(x)的单调递增区间是[kπ+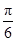 ,kπ+
,kπ+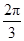 ](k∈Z);
](k∈Z);
⑤存在经过点(a,b)的直线与函数f(x)的图象不相交.
以上结论正确的是 (写出所有正确结论的编号).
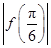 对一切x∈R恒成立,则
对一切x∈R恒成立,则①f
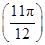 =0;
=0;②︱f
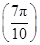 ︱<︱f
︱<︱f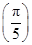 ︱;
︱; ③f(x)既不是奇函数也不是偶函数;
④f(x)的单调递增区间是[kπ+
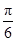 ,kπ+
,kπ+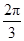 ](k∈Z);
](k∈Z);⑤存在经过点(a,b)的直线与函数f(x)的图象不相交.
以上结论正确的是 (写出所有正确结论的编号).
①③
因为f(x)≤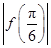 对一切x∈R恒成立,
对一切x∈R恒成立,
所以f(x)的最大值为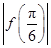 =︱
=︱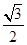 a+
a+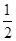 b︱=
b︱=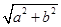 ,
,
两边平方并整理,得
(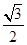 b-
b-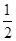 a)2=0,
a)2=0,
所以a=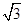 b,
b,
故f(x)=2bsin(2x+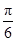 ),
),
所以f(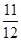 π)=0,
π)=0,
︱f(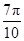 )︱=︱f(
)︱=︱f(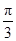 )︱,
)︱,
所以①正确,②错误.
由于b≠0,所以③成立.
当b>0时,递增区间为[kπ-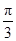 ,kπ+
,kπ+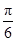 ](k∈Z).
](k∈Z).
又|b|<2|b|,所以⑤不成立.
故正确结论的编号为①③.
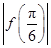 对一切x∈R恒成立,
对一切x∈R恒成立,所以f(x)的最大值为
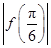 =︱
=︱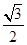 a+
a+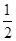 b︱=
b︱=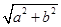 ,
,两边平方并整理,得
(
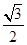 b-
b-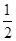 a)2=0,
a)2=0,所以a=
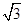 b,
b,故f(x)=2bsin(2x+
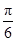 ),
),所以f(
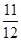 π)=0,
π)=0,︱f(
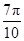 )︱=︱f(
)︱=︱f(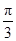 )︱,
)︱,所以①正确,②错误.
由于b≠0,所以③成立.
当b>0时,递增区间为[kπ-
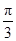 ,kπ+
,kπ+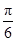 ](k∈Z).
](k∈Z).又|b|<2|b|,所以⑤不成立.
故正确结论的编号为①③.

练习册系列答案
相关题目
 在一个周期内的图像如图所示,其中P,Q分别是这段图像的最高点和最低点,M,N是图像与x轴的交点,且
在一个周期内的图像如图所示,其中P,Q分别是这段图像的最高点和最低点,M,N是图像与x轴的交点,且 ,则A的值为( )
,则A的值为( )



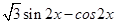 的图象向左平移m个单位(m>一
的图象向左平移m个单位(m>一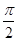 ),若所得的图象关于直线x=
),若所得的图象关于直线x=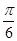 对称,则m的最小值为( )
对称,则m的最小值为( )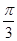
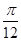
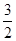 )时,f(x)=sinπx,f
)时,f(x)=sinπx,f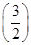 =0,则函数f(x)在区间[0,6]上的零点个数是( )
=0,则函数f(x)在区间[0,6]上的零点个数是( )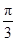 ≤x≤
≤x≤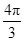 )的最大值与最小值分别为( )
)的最大值与最小值分别为( )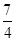 ,最小值为-
,最小值为-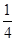
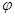 ),x∈R,其中ω>0,-π<
),x∈R,其中ω>0,-π<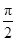 时,f(x)取得最大值,则( )
时,f(x)取得最大值,则( )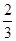 ,求
,求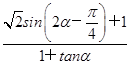 的值.
的值.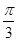 ,则f
,则f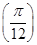 =__________.
=__________.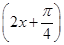 的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的
的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的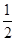 倍,所得图象关于直线x=
倍,所得图象关于直线x=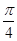 对称.则φ的最小正值为( )
对称.则φ的最小正值为( )