题目内容
11．
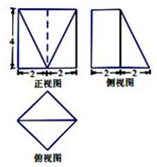若一个几何体的三视图如图所示，则该几何体的体积是（ ）| A． | $\frac{32}{3}$ | B． | $\frac{64}{3}$ | C． | $\frac{80}{3}$ | D． | $\frac{160}{3}$ |
分析 由已知中的三视图，可知该几何体是一个以俯视图为底面的四棱柱切去一个三棱锥所得的几何体，分别柱体体积和锥体体积，相减可得答案．
解答 解：由已知中的三视图，可知该几何体是一个以俯视图为底面的四棱柱切去一个三棱锥所得的几何体，
其直观图如下图所示：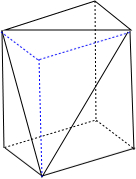
柱体的底面面积S=$\frac{1}{2}×4×4$=8，高为4，体积为32，
锥体的底面面积S=$\frac{1}{2}×$$\frac{1}{2}×4×4$=4，高为4，体积为$\frac{16}{3}$，
故组合体的体积V=32-$\frac{16}{3}$=$\frac{80}{3}$，
故选：C．
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．PM2.5是指空气中直径小于或等于2.5微米的颗粒物（也称可入肺颗粒物）．为了探究车流量与PM2.5的浓度是否相关，现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如下表：
（Ⅰ）根据上表数据，用最小二乘法求出y关于x的线性回归方程$\hat y=\hat bx+\hat a$；
（Ⅱ）若周六同一时间段车流量是25万辆，试根据（Ⅰ）求出的线性回归方程预测，此时PM2.5的浓度为多少（保留整数）？
（参考公式：$\hat b=\frac{{\sum_{i=1}^5{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^5{{{（{x_i}-\overline x）}^2}}}}，\overline y=\hat b•\overline x+\hat a$，参考数据：$\sum_{i=1}^5{x_i}=270，\sum_{i=1}^5{y_i}=370$）
| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x（万辆） | 50 | 51 | 54 | 57 | 58 |
| PM2.5的浓度y（微克/立方米） | 69 | 70 | 74 | 78 | 79 |
（Ⅱ）若周六同一时间段车流量是25万辆，试根据（Ⅰ）求出的线性回归方程预测，此时PM2.5的浓度为多少（保留整数）？
（参考公式：$\hat b=\frac{{\sum_{i=1}^5{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^5{{{（{x_i}-\overline x）}^2}}}}，\overline y=\hat b•\overline x+\hat a$，参考数据：$\sum_{i=1}^5{x_i}=270，\sum_{i=1}^5{y_i}=370$）
19．程序框图如图所示，当A=$\frac{24}{25}$时，输出的k的值为（ ）
| A． | 23 | B． | 24 | C． | 25 | D． | 26 |
16．已知函数f（x）=exsinx，则它在点（4，f（4））处的切线的倾斜角为（ ）
| A． | 0 | B． | 锐角 | C． | $\frac{π}{2}$ | D． | 钝角 |
1．调查某公司的四名推销员，其工作年限与年推销金额如表
由表中数据算出线性回归方程为$\stackrel{∧}{y}$=$\frac{67}{74}$x+$\stackrel{∧}{a}$．若该公司第五名推销员的工作年限为8年，则估计他（她）的年推销金额为$\frac{222}{37}$万元．
| 推销员编号 | 1 | 2 | 3 | 4 |
| 工作年限x/（年） | 3 | 5 | 10 | 14 |
| 年推销金额y/（万元） | 2 | 3 | 7 | 12 |