题目内容
1.调查某公司的四名推销员,其工作年限与年推销金额如表| 推销员编号 | 1 | 2 | 3 | 4 |
| 工作年限x/(年) | 3 | 5 | 10 | 14 |
| 年推销金额y/(万元) | 2 | 3 | 7 | 12 |
分析 根据所给的两组数据,做出x和y的平均数,写出这组数据的样本中心点,根据线性回归方程一定过样本中心点,得到线性回归直线一定过的点的坐标.最后根据第4名推销员的工作年限为6年,即当x=6时,把自变量的值代入线性回归方程,得到y的预报值,即估计出第4名推销员的年推销金额.
解答 解:由条件可知$\overline{x}$=$\frac{1}{4}$(3+5+10+14)=8,$\overline{y}$=$\frac{1}{4}$(2+3+7+12)=6,
代入回归方程,可得a=-$\frac{46}{37}$,所以$\stackrel{∧}{y}$=$\frac{67}{74}$x-$\frac{46}{37}$,
当x=8时,y=$\frac{222}{37}$,
估计他的年推销金额为$\frac{222}{37}$万元.
故答案为:$\frac{222}{37}$.
点评 本题考查线性回归方程的意义,线性回归方程一定过样本中心点,本题解题的关键是正确求出样本中心点,题目的运算量比较小,是一个基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
11.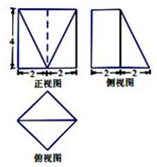 若一个几何体的三视图如图所示,则该几何体的体积是( )
若一个几何体的三视图如图所示,则该几何体的体积是( )
 若一个几何体的三视图如图所示,则该几何体的体积是( )
若一个几何体的三视图如图所示,则该几何体的体积是( )| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | $\frac{80}{3}$ | D. | $\frac{160}{3}$ |
13.P是△AOB所在平面上一点,且在AB的垂直平分线上,若|OA|=3,|OB|=2,则$\overrightarrow{OP}$•$\overrightarrow{AB}$=( )
| A. | $\frac{3}{2}$ | B. | -3 | C. | -$\frac{5}{2}$ | D. | 5 |
11.五个人坐成一排,甲要和乙坐在一起,乙不和丙坐在一起,则不同排法数为( )
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |