题目内容
16．已知函数f（x）=exsinx，则它在点（4，f（4））处的切线的倾斜角为（ ）| A． | 0 | B． | 锐角 | C． | $\frac{π}{2}$ | D． | 钝角 |
分析 求出原函数的导函数，得到f′（4）的符号，即函数f（x）=exsinx在点（4，f（4））处的切线的斜率的符号，则答案可求．
解答 解：由f（x）=exsinx，得f′（x）=exsinx+excosx=ex（sinx+cosx），
∴f′（4）=e4（sin4+cos4），
∵sin4+cos4＜0，∴f′（4）＜0，
∴函数f（x）=exsinx在点（4，f（4））处的切线的倾斜角为钝角．
故选：D．
点评 本题考查利用导数研究过曲线上某点处的切线方程，考查了直线的倾斜角和斜率的关系，是基础题．
练习册系列答案
相关题目
7．函数f（x）为奇函数且f（3x+1）的周期为3，f（1）=-1，则f（2015）=（ ）
| A． | 1 | B． | 0 | C． | -1 | D． | 2 |
11．
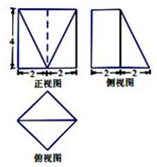若一个几何体的三视图如图所示，则该几何体的体积是（ ）
若一个几何体的三视图如图所示，则该几何体的体积是（ ）| A． | $\frac{32}{3}$ | B． | $\frac{64}{3}$ | C． | $\frac{80}{3}$ | D． | $\frac{160}{3}$ |
8．函数y=log${\;}_{\frac{1}{2}}$（sin2xcos$\frac{π}{4}$-cos2xsin$\frac{π}{4}$）的单调递减区间是（ ）
| A． | （kπ+$\frac{π}{8}$，kπ+$\frac{5π}{8}$），k∈Z | B． | （kπ+$\frac{π}{8}$，kπ+$\frac{3π}{8}$），k∈Z | ||
| C． | （kπ-$\frac{π}{8}$，kπ+$\frac{3π}{8}$），k∈Z | D． | （kπ+$\frac{3π}{8}$，kπ+$\frac{5π}{8}$），k∈Z |
．