题目内容
如图,已知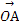 =a,
=a, =b,任意点M关于点A的对称点为S,点S关于点B的对称点为N.设|a|=1,|b|=2,a与b的夹角为30°,若
=b,任意点M关于点A的对称点为S,点S关于点B的对称点为N.设|a|=1,|b|=2,a与b的夹角为30°,若 ⊥(λa+b),则实数λ= .
⊥(λa+b),则实数λ= .

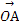 =a,
=a, =b,任意点M关于点A的对称点为S,点S关于点B的对称点为N.设|a|=1,|b|=2,a与b的夹角为30°,若
=b,任意点M关于点A的对称点为S,点S关于点B的对称点为N.设|a|=1,|b|=2,a与b的夹角为30°,若 ⊥(λa+b),则实数λ= .
⊥(λa+b),则实数λ= .

由题意,AB为△SMN的中位线.
所以 =2
=2 .
.
=2( -
-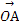 )=2(b-a).
)=2(b-a).
由 ⊥(λa+b),得
⊥(λa+b),得 ·(λa+b)=0,
·(λa+b)=0,
即2(b-a)·(λa+b)=0,
(b-a)·(λa+b)=0,
所以-λa2+b2+(λ-1)a·b=0,
即-λ+4+1×2×cos30°(λ-1)=0,
解得λ= .
.
所以
 =2
=2 .
.=2(
 -
-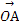 )=2(b-a).
)=2(b-a).由
 ⊥(λa+b),得
⊥(λa+b),得 ·(λa+b)=0,
·(λa+b)=0,即2(b-a)·(λa+b)=0,
(b-a)·(λa+b)=0,
所以-λa2+b2+(λ-1)a·b=0,
即-λ+4+1×2×cos30°(λ-1)=0,
解得λ=
 .
.
练习册系列答案
相关题目
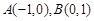 ,点
,点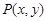 为直线
为直线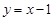 上的一个动点.
上的一个动点.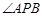 恒为锐角;
恒为锐角;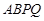 为菱形,求
为菱形,求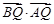 的值.
的值. 与圆
与圆 交于不同的两点
交于不同的两点 ,
, ,且
,且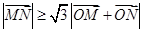 ,其中
,其中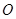 是坐标原点,则实数
是坐标原点,则实数 的取值范围是( )
的取值范围是( )



 =
= +λ·
+λ· (λ∈R),试问:
(λ∈R),试问: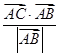 =1,
=1,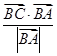 =2,则AB边的长度为( )
=2,则AB边的长度为( )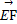 =m
=m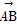 +n
+n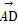 (m,n∈R),则
(m,n∈R),则 的值为( )
的值为( )
 =
= ,且|
,且| |;
|; +
+ +
+ =0;
=0; =-5e1,且|
=-5e1,且| |,则四边形ABCD是等腰梯形;
|,则四边形ABCD是等腰梯形; |=5,则3≤|
|=5,则3≤|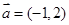 ,
,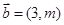 ,
,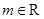 ,则“
,则“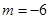 ”是“
”是“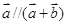 ”的( )
”的( )