题目内容
已知a=(cosθ,1,sinθ),b=(sinθ,1,cosθ),则向量a+b与a-b的夹角是( )
| A.0° | B.30° | C.60° | D.90° |
D
∵a+b=(cosθ+sinθ,2,sinθ+cosθ),
a-b=(cosθ-sinθ,0,sinθ-cosθ).
∴(a+b)·(a-b)=(cosθ+sinθ)(cosθ-sinθ)+2×0+(sinθ+cosθ)·
(sinθ-cosθ)=cos2θ-sin2θ+sin2θ-cos2θ=0.
∴(a+b)⊥(a-b).
即向量a+b与a-b的夹角是90°.
a-b=(cosθ-sinθ,0,sinθ-cosθ).
∴(a+b)·(a-b)=(cosθ+sinθ)(cosθ-sinθ)+2×0+(sinθ+cosθ)·
(sinθ-cosθ)=cos2θ-sin2θ+sin2θ-cos2θ=0.
∴(a+b)⊥(a-b).
即向量a+b与a-b的夹角是90°.

练习册系列答案
相关题目
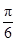 ,则
,则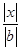 的最大值等于 .
的最大值等于 .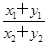 的值为( )
的值为( )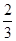
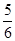
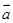 、
、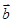 是两个非零向量,则使
是两个非零向量,则使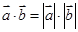 成立的一个必要非充分的条件是( )
成立的一个必要非充分的条件是( )



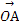 =a,
=a, =b,任意点M关于点A的对称点为S,点S关于点B的对称点为N.设|a|=1,|b|=2,a与b的夹角为30°,若
=b,任意点M关于点A的对称点为S,点S关于点B的对称点为N.设|a|=1,|b|=2,a与b的夹角为30°,若 ⊥(λa+b),则实数λ= .
⊥(λa+b),则实数λ= .
 =m
=m +n
+n ,且点P落在第Ⅲ部分,则实数m,n满足( )
,且点P落在第Ⅲ部分,则实数m,n满足( )
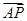 =2
=2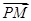 ,则
,则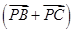 等于( ).
等于( ).

 中,
中, ,
, ,
, ,则
,则
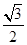


 =a,
=a, =b,则
=b,则 =________.
=________.