题目内容
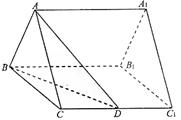
(本题共12分)如图所示,四边形ABCD是矩形,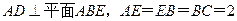 ,F为CE上的点,且BF
,F为CE上的点,且BF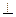 平面ACE,AC与BD交于点G
平面ACE,AC与BD交于点G
(1)AE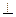 平面BCE
平面BCE
(2)AE//平面BFD
(3)锥C-BGF的体积
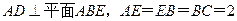 ,F为CE上的点,且BF
,F为CE上的点,且BF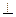 平面ACE,AC与BD交于点G
平面ACE,AC与BD交于点G(1)AE
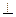 平面BCE
平面BCE(2)AE//平面BFD
(3)锥C-BGF的体积
(1)略
(2)略
(3)三棱锥C-BGF的体积为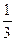
(2)略
(3)三棱锥C-BGF的体积为
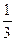
解:(1)∵ 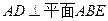 又知四边形ABCD是矩形,故
又知四边形ABCD是矩形,故 AD//BC
AD//BC
∴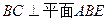 故可知
故可知 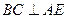 ………….1分
………….1分
∵ BF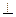 平面ACE ∴ BF
平面ACE ∴ BF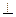 AE …………………………………………2分
AE …………………………………………2分
又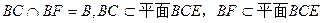
∴ AE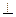 平面BCE …………………………………………………………
平面BCE ………………………………………………………… ……4分
……4分
(2) 依题意,易知G为AC的中点
又∵ BF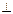 平面ACE 所以可知 BF
平面ACE 所以可知 BF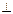 EC, 又BE=EC
EC, 又BE=EC
∴ 可知F为CE的中点 ……………………………………………………………5分
故可知 GF//AE ……………………………………………………………………6分
又可知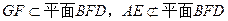
∴ AE//平面BFD……………………………………………………………………..8分
(3) 由(1)可知AE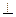 平面BCE,又AE//GF
平面BCE,又AE//GF
∴ GF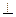 平面BCE……………………………………………………………………9分
平面BCE……………………………………………………………………9分
又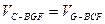 所以GF的长为三棱锥G-BCF的高 GF=
所以GF的长为三棱锥G-BCF的高 GF=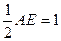 . ....10分
. ....10分
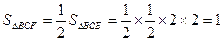 ………………………………………………11分
………………………………………………11分
∴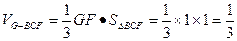
∴ 三棱锥C-BGF的体积为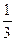 ……………………………………………………..12分
……………………………………………………..12分
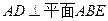 又知四边形ABCD是矩形,故
又知四边形ABCD是矩形,故 AD//BC
AD//BC∴
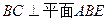 故可知
故可知 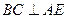 ………….1分
………….1分∵ BF
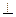 平面ACE ∴ BF
平面ACE ∴ BF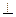 AE …………………………………………2分
AE …………………………………………2分又
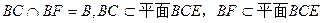
∴ AE
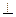 平面BCE …………………………………………………………
平面BCE ………………………………………………………… ……4分
……4分(2) 依题意,易知G为AC的中点
又∵ BF
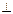 平面ACE 所以可知 BF
平面ACE 所以可知 BF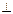 EC, 又BE=EC
EC, 又BE=EC∴ 可知F为CE的中点 ……………………………………………………………5分
故可知 GF//AE ……………………………………………………………………6分
又可知
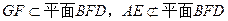
∴ AE//平面BFD……………………………………………………………………..8分
(3) 由(1)可知AE
 平面BCE,又AE//GF
平面BCE,又AE//GF∴ GF
 平面BCE……………………………………………………………………9分
平面BCE……………………………………………………………………9分又
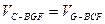 所以GF的长为三棱锥G-BCF的高 GF=
所以GF的长为三棱锥G-BCF的高 GF=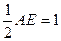 . ....10分
. ....10分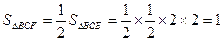 ………………………………………………11分
………………………………………………11分∴
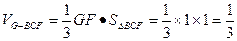
∴ 三棱锥C-BGF的体积为
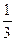 ……………………………………………………..12分
……………………………………………………..12分
练习册系列答案
相关题目
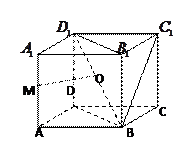
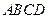 —
—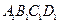 中.
中.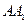 的中点,点
的中点,点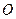 是
是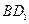 的中点.
的中点.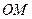 垂直于平面
垂直于平面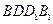 ;
;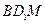 与平面
与平面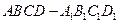 中,
中,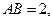
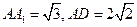 ,
,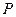 为
为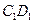 的中点,
的中点,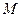 为
为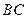 的中点.
的中点.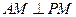 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.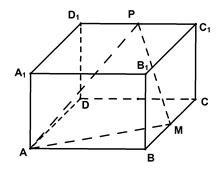
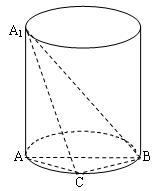
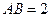 ,
,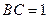 ,设AE与平面ABC所成的角为
,设AE与平面ABC所成的角为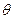 ,且
,且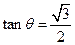 ,
, 平面ABC.
平面ABC.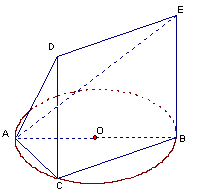
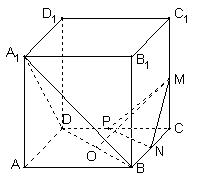
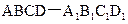 中,M,N,
中,M,N, P分别是
P分别是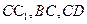 的中点,O为底面ABCD的中心.
的中点,O为底面ABCD的中心.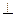 平面
平面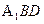 ;
;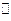 平面
平面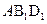 ;
;
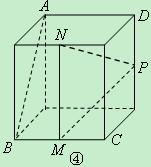
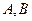 为正方形的两个顶点,
为正方形的两个顶点,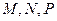 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出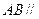 面
面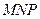 的图形的序号是 .(写出所有符合要求的图形序号)
的图形的序号是 .(写出所有符合要求的图形序号)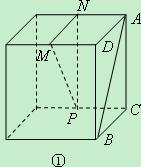
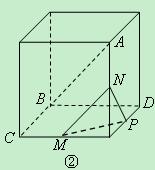
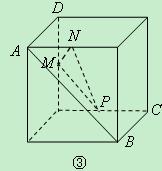
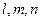 为不同的直线,
为不同的直线,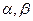 为不同的平面,有如下四个命题:
为不同的平面,有如下四个命题: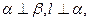 则
则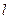 ∥
∥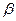 ②若
②若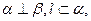 则
则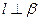
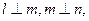 则
则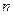 ④若
④若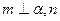 ∥
∥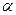 ∥
∥