题目内容
(本题12分)
在单位正方体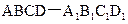 中,M,N,
中,M,N, P分别是
P分别是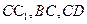 的中点,O为底面ABCD的中心.
的中点,O为底面ABCD的中心.
( 1)求证:OM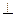 平面
平面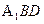 ;
;
(2)平面MNP 平面
平面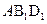 ;
;
(3)求B到平面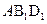 的距离
的距离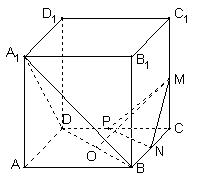
在单位正方体
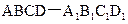 中,M,N,
中,M,N, P分别是
P分别是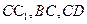 的中点,O为底面ABCD的中心.
的中点,O为底面ABCD的中心.( 1)求证:OM
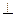 平面
平面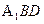 ;
;(2)平面MNP
 平面
平面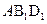 ;
;(3)求B到平面
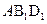 的距离
的距离
(1)略
(2)略
(3)
(2)略
(3)

略

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
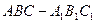 的侧棱长和底面边长均为2, N为侧棱
的侧棱长和底面边长均为2, N为侧棱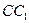 上的点,若平面
上的点,若平面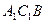 与平面
与平面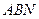 所成二面角(锐角)的余弦值为
所成二面角(锐角)的余弦值为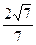 ,试确定点N的位置。
,试确定点N的位置。
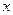
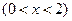 的小正方形,剰余部分围成一个长方体,该长方体的高是小正方形的边长.
的小正方形,剰余部分围成一个长方体,该长方体的高是小正方形的边长.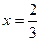 时,Vl取最大值
时,Vl取最大值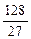 ,为了材料浪费最少,工人师傅还实践出了其它焊接方法,请写出与(1)的焊接方法更佳(使材料浪费最少,容积比Vl大)的设计方案,并计算利用你的设计方案所得到的容器的容积。
,为了材料浪费最少,工人师傅还实践出了其它焊接方法,请写出与(1)的焊接方法更佳(使材料浪费最少,容积比Vl大)的设计方案,并计算利用你的设计方案所得到的容器的容积。
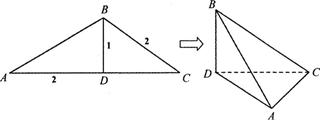
 中,
中,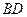 为AC边上的高,
为AC边上的高,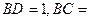
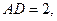 沿BD将
沿BD将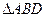 翻折,使得
翻折,使得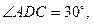 得到几何体
得到几何体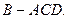
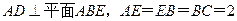 ,F为CE上的点,且BF
,F为CE上的点,且BF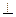 平面ACE,AC与BD交于点G
平面ACE,AC与BD交于点G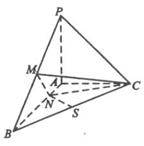
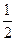 AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.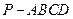 中,
中,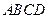 是矩形,三角形PAD为等腰直角三角形,
是矩形,三角形PAD为等腰直角三角形,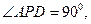 面
面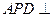 面
面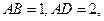
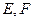 分别为
分别为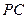 和
和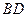 的中点。
的中点。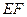 ∥平面
∥平面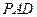 ;
;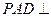 平面
平面 ;
;
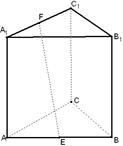
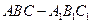 的各棱长都为2,E,F分别是
的各棱长都为2,E,F分别是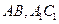 的中点,则EF的长是 ( )
的中点,则EF的长是 ( )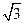
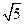
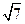
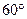 圈上有A、B两点,它们的经度相差
圈上有A、B两点,它们的经度相差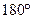 ,A、B两地沿纬线圈的弧长与A、B两点的球面距离的比为( )
,A、B两地沿纬线圈的弧长与A、B两点的球面距离的比为( )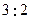 B.
B. 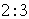 C.
C. 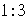 D.
D.