题目内容
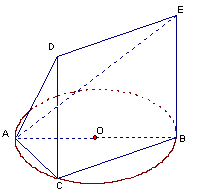
(14分)如图,△ABC内接于圆O,AB是圆O的直径,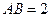 ,
,
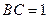 ,设AE与平面ABC所成的角为
,设AE与平面ABC所成的角为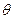 ,且
,且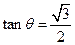 ,
,
四边形DCBE为平行四边形,DC 平面ABC.
平面ABC.
(1)求三棱锥C-ABE的体积;
(2)证明:平面ACD 平面ADE;
平面ADE;
(3)在CD上是否存在一点M,使得MO//平面ADE?证明你的结论.
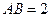 ,
,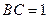 ,设AE与平面ABC所成的角为
,设AE与平面ABC所成的角为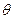 ,且
,且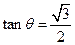 ,
,四边形DCBE为平行四边形,DC
 平面ABC.
平面ABC.(1)求三棱锥C-ABE的体积;
(2)证明:平面ACD
 平面ADE;
平面ADE;(3)在CD上是否存在一点M,使得MO//平面ADE?证明你的结论.

(1)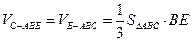
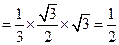
(2)略
(3)略
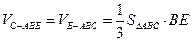
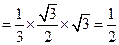
(2)略
(3)略
解:(1)∵四边形DCBE为平行四边形 ∴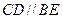
∵ DC 平面ABC ∴
平面ABC ∴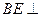 平面ABC
平面ABC
∴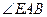 为AE与平面ABC所成的角,
为AE与平面ABC所成的角,
即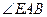 =
=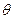 --------------------2分
--------------------2分
在Rt△ABE中,由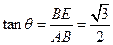 ,
,
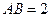 得
得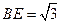 ------------3分
------------3分
∵AB是圆O的直径 ∴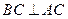
∴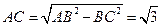
 ∴
∴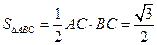 ……………………………………………………4分
……………………………………………………4分
∴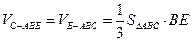
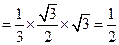 ……………………………………5分
……………………………………5分
(2)证明:∵ DC 平面ABC ,
平面ABC ,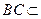 平面ABC ∴
平面ABC ∴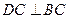 .…………………6分
.…………………6分
∵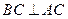 且
且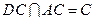 ∴
∴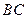
 平面ADC.
平面ADC.
∵DE//BC ∴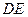
 平面ADC …………………………………………8分
平面ADC …………………………………………8分
又∵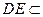 平面ADE ∴平面ACD
平面ADE ∴平面ACD 平面
平面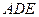 …………………………9分
…………………………9分
(3)在CD上存在点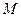 ,使得MO∥平面
,使得MO∥平面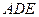 ,该点
,该点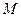 为
为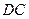 的中点.…… 10分
的中点.…… 10分
证明如下:
如图,取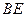 的中点
的中点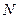 ,连MO、MN、NO,
,连MO、MN、NO,
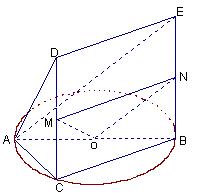
∵M、N、O分别为CD、BE、AB的中点,
∴.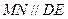 …………………………………………………………11分
…………………………………………………………11分
∵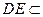 平面ADE,
平面ADE,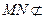 平面ADE,
平面ADE,
∴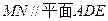 …………………………………………………………12分
…………………………………………………………12分
同理可得NO//平面ADE.
∵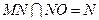 ,∴平面MNO//平面ADE.……………………………………13分
,∴平面MNO//平面ADE.……………………………………13分
∵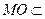 平面MNO,∴MO//平面ADE.……………… 14分(其它证法请参照给分)
平面MNO,∴MO//平面ADE.……………… 14分(其它证法请参照给分)
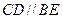
∵ DC
 平面ABC ∴
平面ABC ∴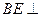 平面ABC
平面ABC∴
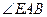 为AE与平面ABC所成的角,
为AE与平面ABC所成的角,即
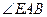 =
=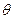 --------------------2分
--------------------2分在Rt△ABE中,由
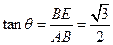 ,
,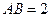 得
得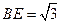 ------------3分
------------3分∵AB是圆O的直径 ∴
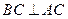
∴
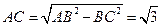
 ∴
∴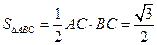 ……………………………………………………4分
……………………………………………………4分∴
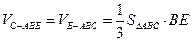
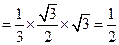 ……………………………………5分
……………………………………5分(2)证明:∵ DC
 平面ABC ,
平面ABC ,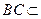 平面ABC ∴
平面ABC ∴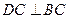 .…………………6分
.…………………6分∵
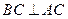 且
且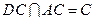 ∴
∴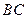
 平面ADC.
平面ADC. ∵DE//BC ∴
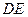
 平面ADC …………………………………………8分
平面ADC …………………………………………8分又∵
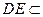 平面ADE ∴平面ACD
平面ADE ∴平面ACD 平面
平面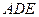 …………………………9分
…………………………9分(3)在CD上存在点
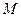 ,使得MO∥平面
,使得MO∥平面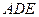 ,该点
,该点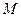 为
为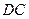 的中点.…… 10分
的中点.…… 10分 证明如下:
如图,取
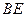 的中点
的中点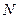 ,连MO、MN、NO,
,连MO、MN、NO,
∵M、N、O分别为CD、BE、AB的中点,
∴.
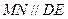 …………………………………………………………11分
…………………………………………………………11分∵
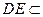 平面ADE,
平面ADE,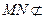 平面ADE,
平面ADE,∴
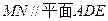 …………………………………………………………12分
…………………………………………………………12分同理可得NO//平面ADE.
∵
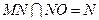 ,∴平面MNO//平面ADE.……………………………………13分
,∴平面MNO//平面ADE.……………………………………13分∵
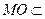 平面MNO,∴MO//平面ADE.……………… 14分(其它证法请参照给分)
平面MNO,∴MO//平面ADE.……………… 14分(其它证法请参照给分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
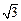 ,∠ACB=90°。
,∠ACB=90°。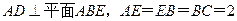 ,F为CE上的点,且BF
,F为CE上的点,且BF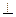 平面ACE,AC与BD交于点G
平面ACE,AC与BD交于点G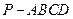 中,
中, 是矩形,三角形PAD为等腰直角三角形,
是矩形,三角形PAD为等腰直角三角形,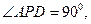 面
面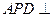 面
面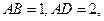
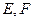 分别为
分别为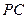 和
和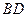 的中点。
的中点。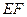 ∥平面
∥平面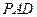 ;
;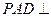 平面
平面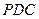 ;
;
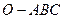 中,
中,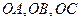 两两垂直,
两两垂直,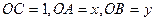 ,且
,且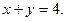 求三棱锥体积的最大值。
求三棱锥体积的最大值。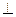 面ABC,BC
面ABC,BC P,使得CP
P,使得CP
 ,
,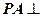 平面
平面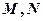 分别是
分别是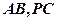 的中点,
的中点,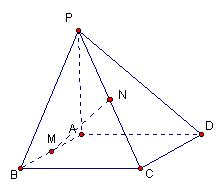
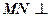 直线
直线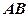 ,
,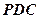 与平面
与平面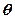 ,能否确定
,能否确定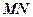 是异面直线
是异面直线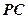 的公垂线.若能确定,求出
的公垂线.若能确定,求出 ABC中,两直角边分别为a,b,斜边上的高为h,则得
ABC中,两直角边分别为a,b,斜边上的高为h,则得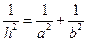 ”由此可类比出命题“若三棱锥S-ABC的三条侧棱SA,SB,SC两两垂直,长分别为a,b,c,底面ABC上的高为h,则得____________________.
”由此可类比出命题“若三棱锥S-ABC的三条侧棱SA,SB,SC两两垂直,长分别为a,b,c,底面ABC上的高为h,则得____________________.