题目内容
如图所示:四棱锥P-ABCD底面一直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点.
(1)证明:EB∥平面PAD;
(2)若PA=AD,证明:BE⊥平面PDC;
(3)当PA=AD=DC时,求二面角E-BD-C的正切值.
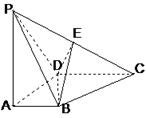
(1)证明:EB∥平面PAD;
(2)若PA=AD,证明:BE⊥平面PDC;
(3)当PA=AD=DC时,求二面角E-BD-C的正切值.

(1)证明见解析(2)证明见解析(3)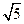
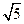
(1)取PD中点Q,连EQ、AQ,则∵QE∥CD,CD∥AB,∴QE∥AB,
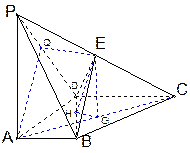
又 ∥AQ
∥AQ
又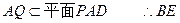 ∥平面PAD…3分
∥平面PAD…3分
(2)PA⊥底面ABCD ∴CD⊥PA,又CD⊥AD
∴CD⊥平面PAD ∴AQ⊥CD若PA=AD,
∴Q为PD中点,∴AQ⊥PD ∴AQ⊥平面PCD
∵BE∥AQ,∴BE⊥平面PCD…………………7分
(3)连结AC,取AC的中点G,连EG,EG∥PA,
∵PA⊥平面ABCD,∴EC⊥平面ABCD,过G作GH⊥BD,连EH,则EH⊥BD,
∴∠EHG是二面角E—BD—C的平面角.
设AB=1,则PA="AD=DC=2AB=2." ∴
又
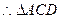 ∽△ABG,
∽△ABG,
 ∴BG∥AD,∠GBH=∠ADB,∴△ABD∽△HBG.
∴BG∥AD,∠GBH=∠ADB,∴△ABD∽△HBG.
 .
.

又
 ∥AQ
∥AQ又
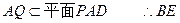 ∥平面PAD…3分
∥平面PAD…3分(2)PA⊥底面ABCD ∴CD⊥PA,又CD⊥AD
∴CD⊥平面PAD ∴AQ⊥CD若PA=AD,
∴Q为PD中点,∴AQ⊥PD ∴AQ⊥平面PCD
∵BE∥AQ,∴BE⊥平面PCD…………………7分
(3)连结AC,取AC的中点G,连EG,EG∥PA,
∵PA⊥平面ABCD,∴EC⊥平面ABCD,过G作GH⊥BD,连EH,则EH⊥BD,
∴∠EHG是二面角E—BD—C的平面角.
设AB=1,则PA="AD=DC=2AB=2." ∴

又

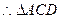 ∽△ABG,
∽△ABG,
 ∴BG∥AD,∠GBH=∠ADB,∴△ABD∽△HBG.
∴BG∥AD,∠GBH=∠ADB,∴△ABD∽△HBG. .
.
练习册系列答案
相关题目
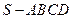 中,底面
中,底面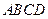 是正方形,
是正方形,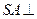 底面
底面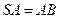 , 点
, 点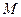 是
是 的中点,
的中点, ,且交
,且交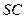 于点
于点 .
.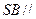 平面
平面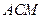 ;
; 的余弦值大小;
的余弦值大小;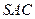 ⊥平面
⊥平面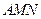 .
.
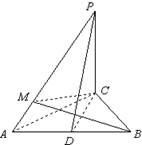
 ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面 ;
;
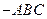 中
中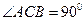 ,
,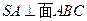 ,
,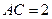 ,
,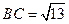 ,
,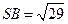 。
。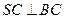 。
。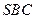 与底面
与底面 所成二面角的大小。
所成二面角的大小。 底面ABCD,E是PC的中点.
底面ABCD,E是PC的中点.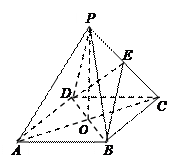
 中,
中,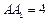 ,
,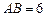 ,点
,点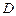 、
、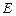 、
、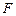 分别在棱
分别在棱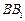 、
、 、
、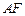 上,且
上,且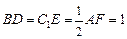 .
. 与平面
与平面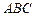 所成锐二面角的大小;
所成锐二面角的大小; 到平面
到平面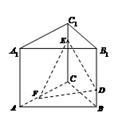
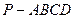 中,
中,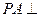 底面
底面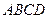 ,
,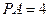 正方形的边长为2
正方形的边长为2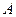 到平面
到平面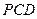 的距离;
的距离;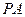 与平面
与平面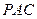 为半平面的二面角的正切值。
为半平面的二面角的正切值。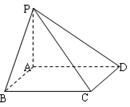
 ABCD底面是直角梯形,
ABCD底面是直角梯形, 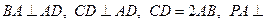 底面ABCD, E为PC的中点, PA=AD=AB=1.
底面ABCD, E为PC的中点, PA=AD=AB=1. 
 ;
; ;
;