题目内容
如图,O是正方形ABCD的中心,PO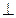 底面ABCD,E是PC的中点.
底面ABCD,E是PC的中点.
求证:⑴PA∥平面BDE;
⑵平面PAC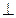 平面BDE.
平面BDE.
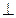 底面ABCD,E是PC的中点.
底面ABCD,E是PC的中点.求证:⑴PA∥平面BDE;
⑵平面PAC
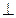 平面BDE.
平面BDE. 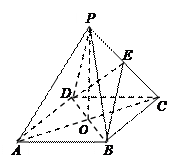 |
见解析
(1)连结EO,在△PAC中,∵O是AC的中点,E是PC的中点,
∴OE∥AP.又∵OE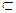 平面BDE,PA
平面BDE,PA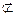 平面BDE,∴PA∥平面BDE.
平面BDE,∴PA∥平面BDE.
(2)∵PO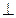 底面ABCD,∴PO
底面ABCD,∴PO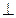 BD.
BD.
又∵AC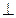 BD,且AC
BD,且AC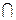 PO=O,∴BD
PO=O,∴BD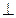 平面PAC.
平面PAC.
而BD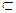 平面BDE,∴平面PAC
平面BDE,∴平面PAC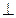 平面BDE.
平面BDE.
∴OE∥AP.又∵OE
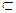 平面BDE,PA
平面BDE,PA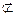 平面BDE,∴PA∥平面BDE.
平面BDE,∴PA∥平面BDE. (2)∵PO
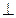 底面ABCD,∴PO
底面ABCD,∴PO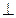 BD.
BD.又∵AC
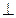 BD,且AC
BD,且AC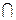 PO=O,∴BD
PO=O,∴BD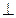 平面PAC.
平面PAC.而BD
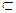 平面BDE,∴平面PAC
平面BDE,∴平面PAC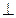 平面BDE.
平面BDE.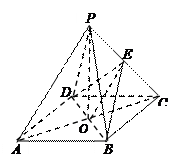 |

练习册系列答案
相关题目
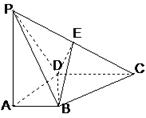
 a,BC=DE=a,
a,BC=DE=a, (1)求证:PA⊥平面ABCDE;
(1)求证:PA⊥平面ABCDE; 平面PDE
平面PDE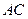 与
与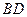 交于点
交于点 ,且
,且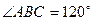 ,M为BC的中点.将此菱形沿对角线BD折成二面角
,M为BC的中点.将此菱形沿对角线BD折成二面角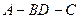 .
.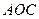
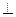 面
面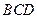 ;(II)若二面角
;(II)若二面角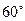 时,求直线
时,求直线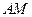 与面
与面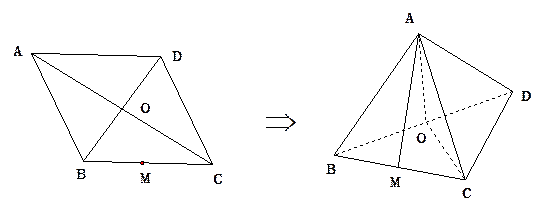
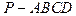 中,AD∥BC,∠ABC=90°,且
中,AD∥BC,∠ABC=90°,且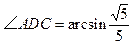 ,又PA⊥平面ABCD,AD=3AB=3PA=3a。
,又PA⊥平面ABCD,AD=3AB=3PA=3a。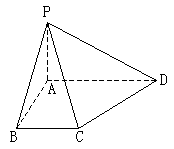
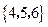 .
.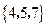 .
.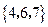 .
.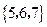 .
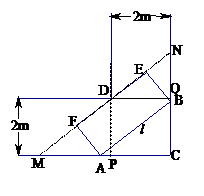
.
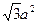
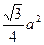

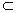 α,b
α,b