题目内容
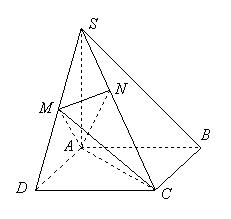
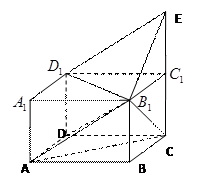
如图,在四棱锥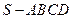 中,底面
中,底面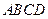 是正方形,
是正方形,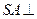 底面
底面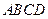 ,
,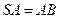 , 点
, 点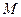 是
是 的中点,
的中点, ,且交
,且交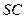 于点
于点 .
.
(I)求证: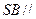 平面
平面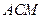 ;
;
(II)求二面角 的余弦值大小;
的余弦值大小;
(III)求证:平面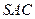 ⊥平面
⊥平面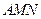 .
.
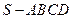 中,底面
中,底面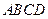 是正方形,
是正方形,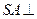 底面
底面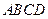 ,
,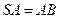 , 点
, 点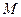 是
是 的中点,
的中点, ,且交
,且交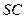 于点
于点 .
.(I)求证:
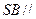 平面
平面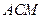 ;
;(II)求二面角
 的余弦值大小;
的余弦值大小;(III)求证:平面
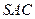 ⊥平面
⊥平面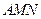 .
.
(Ⅰ)证明见解析(II)二面角 的余弦值为
的余弦值为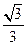 .(III)证明见解析
.(III)证明见解析
 的余弦值为
的余弦值为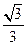 .(III)证明见解析
.(III)证明见解析(Ⅰ)证明:连结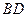 交
交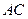 于
于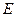 ,连结
,连结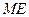 .
.
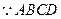 是正方形,∴
是正方形,∴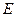 是
是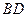 的中点. ----------1分
的中点. ----------1分
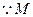 是
是 的中点,∴
的中点,∴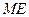 是
是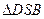 的中位线. ∴
的中位线. ∴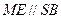 . ----------2分
. ----------2分
又∵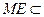 平面
平面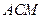 ,
,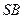
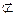 平面
平面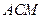 ,----------3分
,----------3分
∴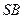
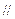 平面
平面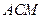 .------------------4分
.------------------4分
(II)如图,以A为坐标原点,建立空间直角坐标系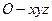 ,
,
由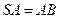 故设
故设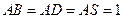 ,则
,则

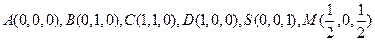 . ----------6分
. ----------6分
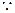
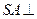 底面
底面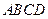 ,
,
∴ 是平面
是平面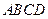 的法向量,
的法向量,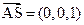 .----------7分
.----------7分
设平面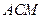 的法向量为
的法向量为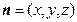 ,
,
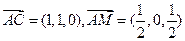 ,
,
则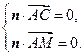 即
即
∴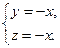 令
令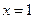 ,则
,则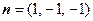 . ----------9分
. ----------9分
∴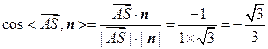 ,
,
∴二面角 的余弦值为
的余弦值为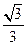 .------------------10分
.------------------10分
(III)
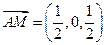 ,
,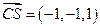 ,
,
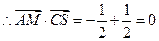 ----------11分
----------11分
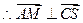 又
又 且
且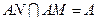 .----------12分
.----------12分
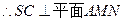 . 又
. 又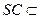 平面
平面 ----------13分
----------13分
∴平面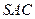 ⊥平面
⊥平面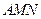 . ------------------14分
. ------------------14分
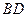 交
交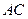 于
于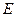 ,连结
,连结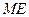 .
. 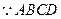 是正方形,∴
是正方形,∴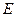 是
是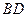 的中点. ----------1分
的中点. ----------1分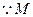 是
是 的中点,∴
的中点,∴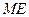 是
是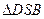 的中位线. ∴
的中位线. ∴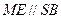 . ----------2分
. ----------2分又∵
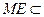 平面
平面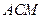 ,
,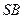
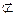 平面
平面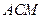 ,----------3分
,----------3分∴
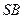
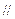 平面
平面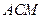 .------------------4分
.------------------4分(II)如图,以A为坐标原点,建立空间直角坐标系
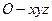 ,
,由
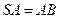 故设
故设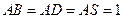 ,则
,则
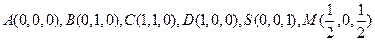 . ----------6分
. ----------6分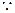
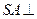 底面
底面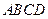 ,
,∴
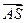 是平面
是平面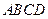 的法向量,
的法向量,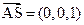 .----------7分
.----------7分设平面
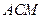 的法向量为
的法向量为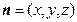 ,
, 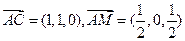 ,
, 则
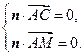 即
即
∴
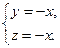 令
令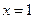 ,则
,则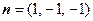 . ----------9分
. ----------9分∴
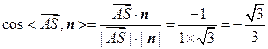 ,
,∴二面角
 的余弦值为
的余弦值为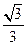 .------------------10分
.------------------10分(III)
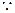
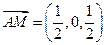 ,
,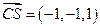 ,
,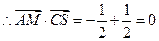 ----------11分
----------11分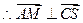 又
又 且
且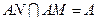 .----------12分
.----------12分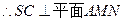 . 又
. 又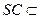 平面
平面 ----------13分
----------13分∴平面
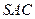 ⊥平面
⊥平面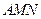 . ------------------14分
. ------------------14分
练习册系列答案
相关题目
 中,点
中,点 在棱
在棱 的延长线上,
的延长线上, .
.
 //平面
//平面 ;
; (Ⅱ) 求证:平面
(Ⅱ) 求证:平面
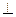 平面
平面 ;
; 的体积.
的体积.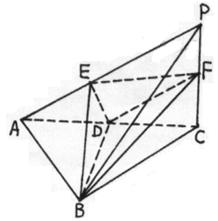
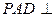 平面ABCD,ABCD为正方形,
平面ABCD,ABCD为正方形,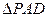 是直角三角形,且
是直角三角形,且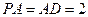 ,E、F、G分别是线段PA,PD,CD的中点.
,E、F、G分别是线段PA,PD,CD的中点.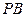 ∥面EFC;
∥面EFC;
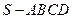 的底面是正方形,
的底面是正方形,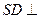 平面
平面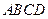 .
.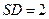 ,
,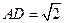 ,
,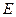 是
是 上的点.
上的点.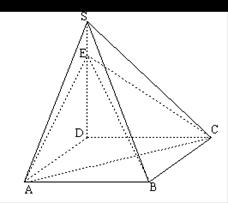
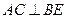 ;
;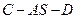 的余弦值.
的余弦值.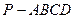 的底面为正方形,
的底面为正方形,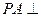 底面
底面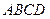 ,
, ,
,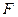 为
为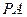 上的点.
上的点. ;
;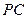 //平面
//平面 ,求二面角
,求二面角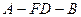 的余弦值.
的余弦值.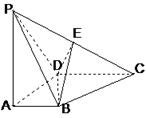
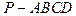 中,AD∥BC,∠ABC=90°,且
中,AD∥BC,∠ABC=90°,且 ,又PA⊥平面ABCD,AD=3AB=3PA=3a。
,又PA⊥平面ABCD,AD=3AB=3PA=3a。