题目内容
如图,PC⊥平面ABC,∠ACB=90°,D为AB中点,
AC=BC=PC=2.
(Ⅰ)求证:AB⊥平面PCD;
(Ⅱ)求异面直线PD与BC所成角的大小;
(Ⅲ)设M为线段PA上的点,且AP=4AM,求点A到平面BCM的距离.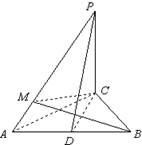
AC=BC=PC=2.
(Ⅰ)求证:AB⊥平面PCD;
(Ⅱ)求异面直线PD与BC所成角的大小;
(Ⅲ)设M为线段PA上的点,且AP=4AM,求点A到平面BCM的距离.

(Ⅰ)证明见解析。
(Ⅱ) arccos
(Ⅲ)
(Ⅱ) arccos

(Ⅲ)

本小题主要考查空间直线与直线、直线与平面的位置关系,异面直线所成的角,点面距离等基础知识;考查空间想象能力、逻辑思维能力和运算能力.满分12分.
(Ⅰ)因为PC⊥平面ABC,AB 平面ABC,所以PC⊥AB.………………………2分
平面ABC,所以PC⊥AB.………………………2分
△ABC中,AC=BC,且D为AB中点,所以CD⊥AB.
又PC∩CD=C,所以AB⊥平面PCD.…………………………………………4分
(Ⅱ)如图,取AC中点E,连结DE、PE,则DE∥BC,
所以∠PDE(或其补角)为异面直线PD与BC所成的角.…………………5分
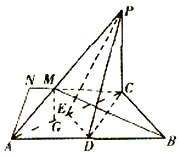 因为BC∥DE,AC⊥BC,所以AC⊥DE;
因为BC∥DE,AC⊥BC,所以AC⊥DE;
又PC⊥平面ABC,DE 平面ABC,所以PC⊥DE,
平面ABC,所以PC⊥DE,
因为AC∩PC=C,所以DE⊥平面PAC,
因为PEC平面PAC,所以DE⊥PE.………6分
在Rt△ABC中,因为AC=BC=2,所以AB=2
在Rt△PCD中,因为PC=2,CD= AB=
AB= ,
,
所以PD= .
.
在Rt△PDE中,因为DE= BC=1.所以cos∠PDE=
BC=1.所以cos∠PDE=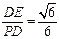
即异面直线PD与BC所成的角为arccos .……………………………8分
.……………………………8分
(Ⅲ)因为BC⊥AC,BC⊥PC,所以BC⊥平面PAC,所以平面PCM⊥平面BCM.
过点A作AN⊥CM交CM于N,则AN⊥平面BCM.…………………10分
在Rt△PAC中,AC=PC=2,所以AP=2 ,又AP=4AM,所以AM=
,又AP=4AM,所以AM=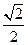
△ACM中,∠MAC=45°,所以CM=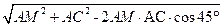 =
=
过M作MG⊥AC交AC于G,MG=AMsin45°= ,
,
由 MG·AC=
MG·AC= AN·CM,得AN=
AN·CM,得AN= .
.
所以点A到平面BCM的距离为 .…………………………………12分
.…………………………………12分
(Ⅰ)因为PC⊥平面ABC,AB
 平面ABC,所以PC⊥AB.………………………2分
平面ABC,所以PC⊥AB.………………………2分△ABC中,AC=BC,且D为AB中点,所以CD⊥AB.
又PC∩CD=C,所以AB⊥平面PCD.…………………………………………4分
(Ⅱ)如图,取AC中点E,连结DE、PE,则DE∥BC,
所以∠PDE(或其补角)为异面直线PD与BC所成的角.…………………5分
 因为BC∥DE,AC⊥BC,所以AC⊥DE;
因为BC∥DE,AC⊥BC,所以AC⊥DE;又PC⊥平面ABC,DE
 平面ABC,所以PC⊥DE,
平面ABC,所以PC⊥DE,因为AC∩PC=C,所以DE⊥平面PAC,
因为PEC平面PAC,所以DE⊥PE.………6分
在Rt△ABC中,因为AC=BC=2,所以AB=2

在Rt△PCD中,因为PC=2,CD=
 AB=
AB= ,
,所以PD=
 .
.在Rt△PDE中,因为DE=
 BC=1.所以cos∠PDE=
BC=1.所以cos∠PDE=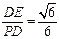
即异面直线PD与BC所成的角为arccos
 .……………………………8分
.……………………………8分(Ⅲ)因为BC⊥AC,BC⊥PC,所以BC⊥平面PAC,所以平面PCM⊥平面BCM.
过点A作AN⊥CM交CM于N,则AN⊥平面BCM.…………………10分
在Rt△PAC中,AC=PC=2,所以AP=2
 ,又AP=4AM,所以AM=
,又AP=4AM,所以AM=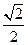
△ACM中,∠MAC=45°,所以CM=
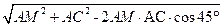 =
=
过M作MG⊥AC交AC于G,MG=AMsin45°=
 ,
,由
 MG·AC=
MG·AC= AN·CM,得AN=
AN·CM,得AN= .
.所以点A到平面BCM的距离为
 .…………………………………12分
.…………………………………12分
练习册系列答案
相关题目
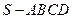 的底面是正方形,
的底面是正方形,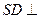 平面
平面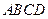 .
.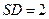 ,
,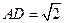 ,
,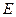 是
是 上的点.
上的点.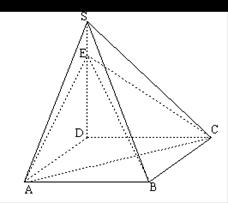
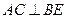 ;
;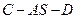 的余弦值.
的余弦值.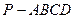 的底面为正方形,
的底面为正方形,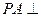 底面
底面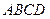 ,
, ,
,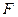 为
为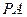 上的点.
上的点. ;
;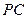 //平面
//平面 ,求二面角
,求二面角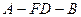 的余弦值.
的余弦值.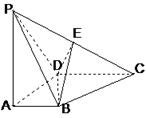
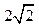 a,BC=DE=a,
a,BC=DE=a,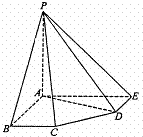 (1)求证:PA⊥平面ABCDE;
(1)求证:PA⊥平面ABCDE;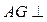 平面PDE
平面PDE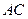 与
与 交于点
交于点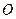 ,且
,且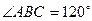 ,M为BC的中点.将此菱形沿对角线BD折成二面角
,M为BC的中点.将此菱形沿对角线BD折成二面角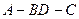 .
.
 面
面 ;(II)若二面角
;(II)若二面角 时,求直线
时,求直线 与面
与面
 ⊥平面
⊥平面 ,那么
,那么 ,平面
,平面 ,那么
,那么 平面
平面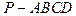 中,AD∥BC,∠ABC=90°,且
中,AD∥BC,∠ABC=90°,且 ,又PA⊥平面ABCD,AD=3AB=3PA=3a。
,又PA⊥平面ABCD,AD=3AB=3PA=3a。
 的顶点
的顶点 在椭圆
在椭圆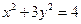 上,对角线
上,对角线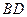 所在直线的斜率为1.
所在直线的斜率为1.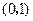 时,求直线
时,求直线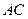 的方程;
的方程; 时,求菱形
时,求菱形