题目内容
在三棱锥S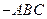 中
中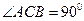 ,
,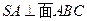 ,
,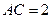 ,
,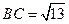 ,
,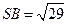 。
。
(1)证明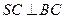 。
。
(2)求侧面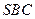 与底面
与底面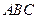 所成二面角的大小。
所成二面角的大小。
(3)求异面直线SC与AB所成角的大小。
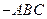 中
中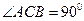 ,
,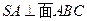 ,
,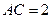 ,
,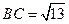 ,
,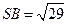 。
。(1)证明
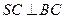 。
。(2)求侧面
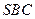 与底面
与底面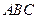 所成二面角的大小。
所成二面角的大小。(3)求异面直线SC与AB所成角的大小。
(1)见解析(2)600(3)

(1)∵∠SAB=∠SCA=900
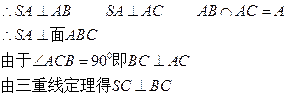
(2)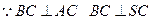
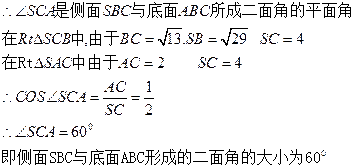
(3)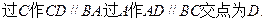
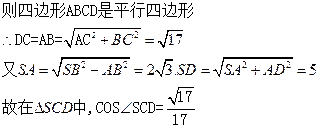

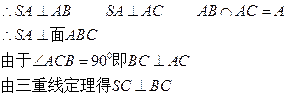
(2)
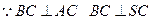
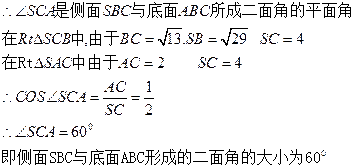
(3)
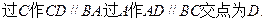
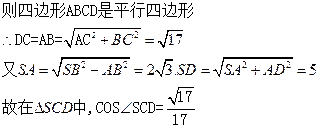


练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
题目内容
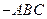 中
中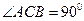 ,
,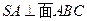 ,
,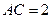 ,
,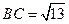 ,
,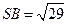 。
。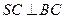 。
。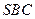 与底面
与底面 所成二面角的大小。
所成二面角的大小。
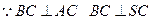
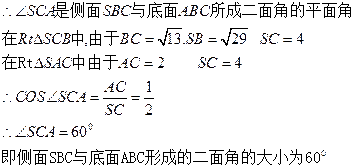
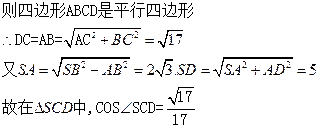


 备战中考寒假系列答案
备战中考寒假系列答案