题目内容
、(12分)已知数列  的前n项和Sn=2n2+2n数列
的前n项和Sn=2n2+2n数列  的前 n 项和 Tn=2-bn
的前 n 项和 Tn=2-bn
(1)求数列 与
与  的通项公式;
的通项公式;
(2)设Cn=an2·bn,证明当且仅当n≥3时,Cn+1<Cn
 的前n项和Sn=2n2+2n数列
的前n项和Sn=2n2+2n数列  的前 n 项和 Tn=2-bn
的前 n 项和 Tn=2-bn(1)求数列
 与
与  的通项公式;
的通项公式;(2)设Cn=an2·bn,证明当且仅当n≥3时,Cn+1<Cn
(1)a1=S1=4
当n≥2时,an=Sn-Sn-1=2n(n+1)-2 (n-1)n=4n
(n-1)n=4n
∴an=4n (n∈N*)
将n=1代入Tn=2-bn得b1=2-b1
∴b1=1
当n≥2时,Tn-1=2bn-1
Tn=2-bn
∴bn=T n-Tn-1=-bn+bn-1
n-Tn-1=-bn+bn-1
∴bn= bn-1
bn-1
故 是以1为首项,
是以1为首项, 为公比的等比数列
为公比的等比数列
∴bn=( )n-1 (n∈N*)
)n-1 (n∈N*)
(2)由Cn = a ·b
·b = n2·25-n
= n2·25-n
∴ =
= 
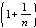 2
2
当且仅当n≥3时,1+ ≤
≤ <
<
即Cn+1<Cn
当n≥2时,an=Sn-Sn-1=2n(n+1)-2
 (n-1)n=4n
(n-1)n=4n∴an=4n (n∈N*)
将n=1代入Tn=2-bn得b1=2-b1
∴b1=1
当n≥2时,Tn-1=2bn-1
Tn=2-bn
∴bn=T
 n-Tn-1=-bn+bn-1
n-Tn-1=-bn+bn-1∴bn=
 bn-1
bn-1故
 是以1为首项,
是以1为首项, 为公比的等比数列
为公比的等比数列∴bn=(
 )n-1 (n∈N*)
)n-1 (n∈N*)(2)由Cn = a
 ·b
·b = n2·25-n
= n2·25-n∴
 =
= 
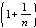 2
2当且仅当n≥3时,1+
 ≤
≤ <
<
即Cn+1<Cn
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
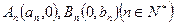 ,其中数列
,其中数列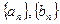 都是递增数列。
都是递增数列。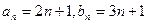 ,判断直线
,判断直线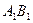 与
与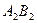 是否平行;
是否平行;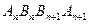 的面积为
的面积为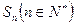 .
.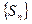 也是等差数列;
也是等差数列;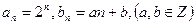 ,
,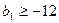 ,记直线
,记直线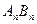 的斜率为
的斜率为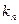 ,数列
,数列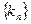 前8项依次递减,求满足条件的数列
前8项依次递减,求满足条件的数列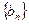 的个数。
的个数。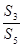 的值为
的值为 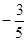
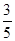
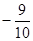

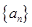 的前
的前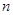 项和为
项和为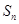 ,若
,若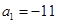 ,
,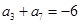 ,则当
,则当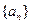 为等比数列,
为等比数列,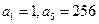 ;
;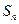 为等差数列
为等差数列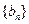 的前n项和,
的前n项和,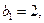
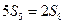 .
.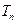
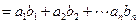 ,求
,求
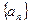 满足a1=2,
满足a1=2,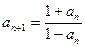 (
(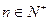 ),则
),则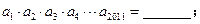
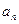 }满足
}满足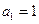 ,且
,且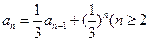 ,且
,且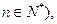 则数列{
则数列{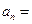
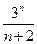
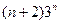
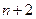
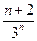
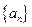 是公差不为零的等差数列,前
是公差不为零的等差数列,前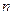 项和为
项和为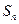 ,满足
,满足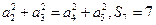 ,则使得
,则使得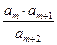 为数列
为数列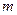 的值为
的值为