题目内容
((本小题满分12分)
已知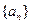 为等比数列,
为等比数列,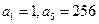 ;
;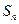 为等差数列
为等差数列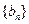 的前n项和,
的前n项和,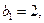
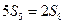 .
.
(1) 求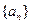 和
和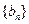 的通项公式;
的通项公式;
(2) 设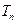
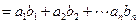 ,求
,求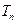 .
.
已知
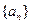 为等比数列,
为等比数列,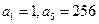 ;
;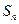 为等差数列
为等差数列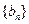 的前n项和,
的前n项和,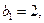
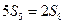 .
.(1) 求
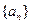 和
和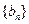 的通项公式;
的通项公式;(2) 设
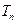
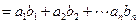 ,求
,求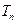 .
.解:(1) 设{an}的公比为q,由a5=a1q4得q=4
所以an=4n-1.…………………………………………………………………………4分
设{ bn }的公差为d,由5S5=2 S8得5(5 b1+10d)=2(8 b1+28d),
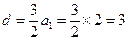 ,
,
所以bn=b1+(n-1)d=3n-1.…………………………………………………8分
(2) Tn=1·2+4·5+42·8+…+4n-1 (3n-1),①
(3n-1),①
4Tn=4·2+42·5+43·8+…+4n(3n-1),②
②-①得:3Tn=-2-3(4+42+…+4n)+4n(3n-1)……………………………10分
= -2+4(1-4n-1)+4n(3n-1)
=2+(3n-2)·4n………………………………………………………12分
∴Tn=(n-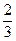 )4n+
)4n+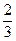
所以an=4n-1.…………………………………………………………………………4分
设{ bn }的公差为d,由5S5=2 S8得5(5 b1+10d)=2(8 b1+28d),
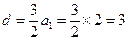 ,
,所以bn=b1+(n-1)d=3n-1.…………………………………………………8分
(2) Tn=1·2+4·5+42·8+…+4n-1
 (3n-1),①
(3n-1),①4Tn=4·2+42·5+43·8+…+4n(3n-1),②
②-①得:3Tn=-2-3(4+42+…+4n)+4n(3n-1)……………………………10分
= -2+4(1-4n-1)+4n(3n-1)
=2+(3n-2)·4n………………………………………………………12分
∴Tn=(n-
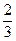 )4n+
)4n+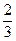
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前n项和Sn=2n2+2n数列
的前n项和Sn=2n2+2n数列  的前 n 项和 Tn=2-bn
的前 n 项和 Tn=2-bn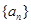 ,其通项公式为
,其通项公式为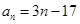 ,则其前n项和
,则其前n项和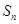 在n为( )时获得最小值
在n为( )时获得最小值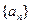 的前n项和
的前n项和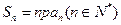 ,并且
,并且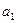 ≠
≠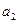 .
.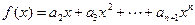 ,如果
,如果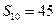 ,证明:
,证明: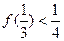 .
. 的前n项和为
的前n项和为 ,且
,且 ,其中p是不为零的常数.
,其中p是不为零的常数. 满足
满足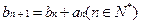 ,
, ,求数列
,求数列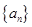 的前
的前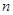 项和为
项和为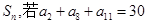 ,那么
,那么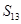 值的是( )
值的是( ) 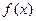 是定义在R上恒不为0的函数,对任意
是定义在R上恒不为0的函数,对任意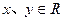 都有
都有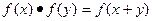 ,
,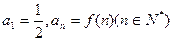 ,则数列
,则数列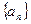 的前n项和Sn的取值范围是
的前n项和Sn的取值范围是 ( )
( )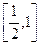
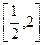
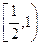
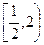
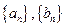 的各项均为正数,若对任意的正整数
的各项均为正数,若对任意的正整数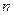 ,都有
,都有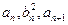 成等差数列,且
成等差数列,且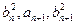 成等比数列.
成等比数列. 是等差数列;
是等差数列;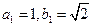 ,求数列。的前。项和。
,求数列。的前。项和。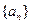 中,已知
中,已知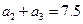 ,
,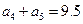 ,则等差数列
,则等差数列