题目内容
设等差数列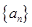 的前
的前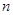 项和为
项和为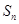 ,若
,若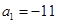 ,
,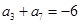 ,则当
,则当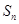 取最小值时,
取最小值时,
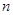 等于
等于
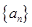 的前
的前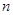 项和为
项和为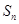 ,若
,若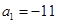 ,
,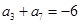 ,则当
,则当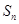 取最小值时,
取最小值时,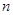 等于
等于| A.8 | B.7 | C. 6 | D.9 |
C
专题:计算题.
分析:根据等差数列的性质化简a3+a7=-6,得到a5的值,然后根据a1的值,利用等差数列的通项公式即可求出公差d的值,根据a1和d的值写出等差数列的通项公式,进而写出等差数列的前n项和公式Sn,配方后即可得到Sn取最小值时n的值.
解答:解:由等差数列的性质可得 a3+a7=2a5=-6,解得a5=-3. 又a1=-11,设公差为d,
所以,a5=a1+4d=-11+4d=-3,解得d=2.
则an=-11+2(n-1)=2n-13,
所以Sn=
 =n2-12n=(n-6)2-36,
=n2-12n=(n-6)2-36,所以当n=6时,Sn取最小值.
故选C.
点评:此题考查学生灵活运用等差数列的通项公式及前n项和公式化简求值,掌握等差数列的性质,是一道中档题.

练习册系列答案
相关题目
 的前n项和Sn=2n2+2n数列
的前n项和Sn=2n2+2n数列  的前 n 项和 Tn=2-bn
的前 n 项和 Tn=2-bn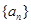 ,其通项公式为
,其通项公式为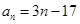 ,则其前n项和
,则其前n项和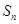 在n为( )时获得最小值
在n为( )时获得最小值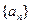 的前n项和
的前n项和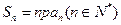 ,并且
,并且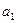 ≠
≠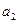 .
.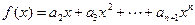 ,如果
,如果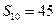 ,证明:
,证明: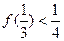 .
. 的前n项和为
的前n项和为 ,且
,且 ,其中p是不为零的常数.
,其中p是不为零的常数. 满足
满足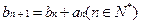 ,
, ,求数列
,求数列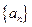 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,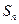 为
为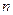 项和.
项和.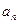 及
及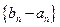 是首项为1,公比为3的等
是首项为1,公比为3的等 比数列,求数列
比数列,求数列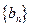 的通项公式及其前
的通项公式及其前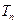 .
.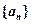 是等差数列,
是等差数列,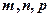 是互不相等的正整数,则有:
是互不相等的正整数,则有: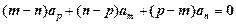 ,类比上述性质,相应地,对等比数列
,类比上述性质,相应地,对等比数列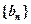 有 。
有 。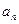 }满足
}满足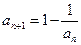
 ,且
,且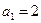 ,则
,则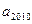 =" " ( )
=" " ( )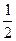

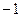
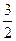
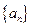 中,
中,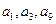 又成等比数列,则
又成等比数列,则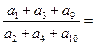
 ___
___