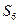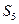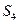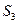题目内容
(本小题满分16分)已知在直角坐标系中,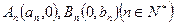 ,其中数列
,其中数列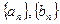 都是递增数列。
都是递增数列。
(1)若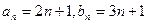 ,判断直线
,判断直线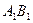 与
与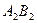 是否平行;
是否平行;
(2)若数列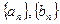 都是正项等差数列,设四边形
都是正项等差数列,设四边形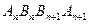 的面积为
的面积为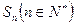 .
.
求证: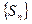 也是等差数列;
也是等差数列;
(3)若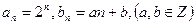 ,
,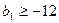 ,记直线
,记直线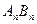 的斜率为
的斜率为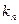 ,数列
,数列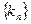 前8项依次递减,求满足条件的数列
前8项依次递减,求满足条件的数列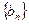 的个数。
的个数。
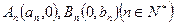 ,其中数列
,其中数列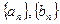 都是递增数列。
都是递增数列。(1)若
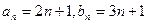 ,判断直线
,判断直线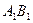 与
与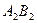 是否平行;
是否平行;(2)若数列
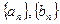 都是正项等差数列,设四边形
都是正项等差数列,设四边形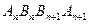 的面积为
的面积为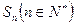 .
.求证:
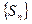 也是等差数列;
也是等差数列;(3)若
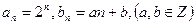 ,
,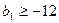 ,记直线
,记直线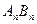 的斜率为
的斜率为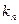 ,数列
,数列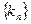 前8项依次递减,求满足条件的数列
前8项依次递减,求满足条件的数列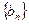 的个数。
的个数。⑴由题意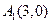 、
、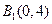 、
、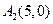 、
、 .
.
∴ ,
, .…………………………………(2分)
.…………………………………(2分)

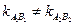 ,∴
,∴ 与
与 不平行. ……………………………………(4分)
不平行. ……………………………………(4分)
⑵
 、
、 为等差数列,设它们的公差分别为
为等差数列,设它们的公差分别为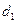 和
和 ,则
,则 ,
,
由题意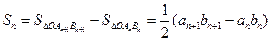 .……………………………(6分)
.……………………………(6分)
∴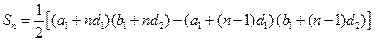
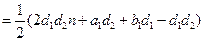 ,……(8分)
,……(8分)
∴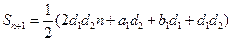 ,∴
,∴ 是与
是与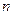 无关的常数,
无关的常数,
∴数列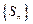 是等差数列.……………………………………………………………(10分)
是等差数列.……………………………………………………………(10分)
⑶

 、
、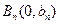 ,∴
,∴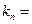
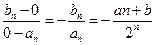 .
.
又数列 前
前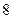 项依次递减,
项依次递减,
∴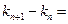

 对
对 成立,即
成立,即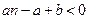 对
对 成立.………………(12分)
成立.………………(12分)
又数列 是递增数列,∴
是递增数列,∴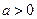 ,只要
,只要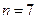 时,即
时,即 即可.
即可.
又 ,联立不等式
,联立不等式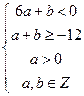 ,作出可行域(如右图所示),易得
,作出可行域(如右图所示),易得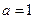 或
或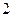 .…………(14分)
.…………(14分)
当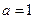 时,
时, ,即
,即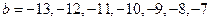 ,有
,有 解;
解;
当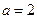 时,
时,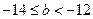 ,即
,即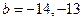 ,有
,有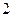 解.∴数列
解.∴数列 共有
共有 个.(16分)
个.(16分)
另解:也可直接由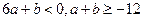 得
得 .又
.又 ,则
,则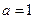 或
或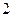 .下同
.下同
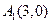 、
、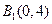 、
、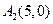 、
、 .
.∴
 ,
, .…………………………………(2分)
.…………………………………(2分)
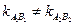 ,∴
,∴ 与
与 不平行. ……………………………………(4分)
不平行. ……………………………………(4分)⑵

 、
、 为等差数列,设它们的公差分别为
为等差数列,设它们的公差分别为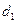 和
和 ,则
,则 ,
,由题意
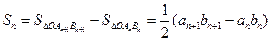 .……………………………(6分)
.……………………………(6分)∴
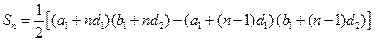
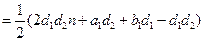 ,……(8分)
,……(8分)∴
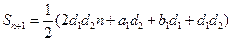 ,∴
,∴ 是与
是与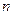 无关的常数,
无关的常数,∴数列
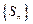 是等差数列.……………………………………………………………(10分)
是等差数列.……………………………………………………………(10分)⑶

 、
、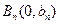 ,∴
,∴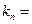
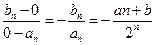 .
.又数列
 前
前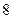 项依次递减,
项依次递减,∴
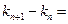

 对
对 成立,即
成立,即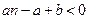 对
对 成立.………………(12分)
成立.………………(12分)又数列
 是递增数列,∴
是递增数列,∴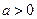 ,只要
,只要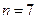 时,即
时,即 即可.
即可.又
 ,联立不等式
,联立不等式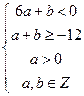 ,作出可行域(如右图所示),易得
,作出可行域(如右图所示),易得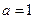 或
或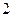 .…………(14分)
.…………(14分)当
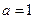 时,
时, ,即
,即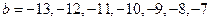 ,有
,有 解;
解;当
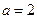 时,
时,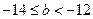 ,即
,即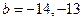 ,有
,有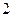 解.∴数列
解.∴数列 共有
共有 个.(16分)
个.(16分)另解:也可直接由
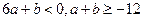 得
得 .又
.又 ,则
,则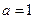 或
或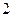 .下同
.下同略

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
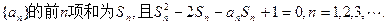
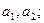
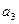 ;
; 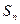 的表达式.
的表达式. 的前n项和Sn=2n2+2n数列
的前n项和Sn=2n2+2n数列  的前 n 项和 Tn=2-bn
的前 n 项和 Tn=2-bn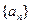 的前n项和
的前n项和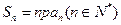 ,并且
,并且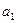 ≠
≠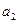 .
.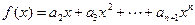 ,如果
,如果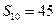 ,证明:
,证明: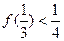 .
.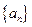 的前
的前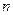 项和为
项和为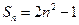 ,则数列
,则数列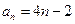
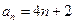
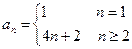
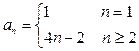
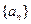 中的前
中的前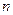 项和为
项和为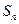 ,已知
,已知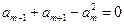 ,
,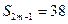 ,则
,则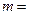 _________
_________ ;
;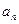 }满足
}满足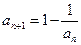
 ,且
,且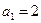 ,则
,则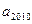 =" " ( )
=" " ( )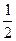

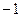
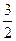
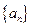 中,
中,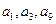 又成等比数列,则
又成等比数列,则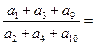
 ___
___ 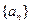 的前n项的乘积
的前n项的乘积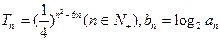 ,则数列
,则数列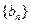 的前n项和
的前n项和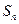 中的最大值是 ( )
中的最大值是 ( )