题目内容
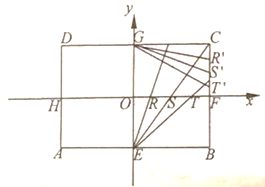
【题目】抛物线M:![]() 的焦点为F,过焦点F的直线l(与x轴不垂直)交抛物线M于点A,B,A关于x轴的对称点为
的焦点为F,过焦点F的直线l(与x轴不垂直)交抛物线M于点A,B,A关于x轴的对称点为![]() .
.
(1)求证:直线![]() 过定点,并求出这个定点;
过定点,并求出这个定点;
(2)若![]() 的垂直平分线交抛物线于C,D,四边形
的垂直平分线交抛物线于C,D,四边形![]() 外接圆圆心N的横坐标为19,求直线AB和圆N的方程.
外接圆圆心N的横坐标为19,求直线AB和圆N的方程.
【答案】(1)见解析,定点![]() ;(2)直线AB:
;(2)直线AB:![]() ,圆N:
,圆N:![]()
【解析】
(1)设直线AB:![]() (
(![]() ),求出
),求出![]() :
:![]() ,令
,令![]() 即得定点坐标;
即得定点坐标;
(2)求出![]() ,再分类讨论,先求出CD方程为:
,再分类讨论,先求出CD方程为:![]() ,再根据线段CD是圆N的直径,求出直线AB和圆N的方程.
,再根据线段CD是圆N的直径,求出直线AB和圆N的方程.
(1)设直线AB:![]() (
(![]() ),代入抛物线方程得:
),代入抛物线方程得:![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
所以![]() ,
,![]() ,
,
从而![]() :
:![]() ,令
,令![]() 得:
得:
![]() ,
,
所以直线![]() 过定点
过定点![]() .
.
(2)由(1)知:![]() ,
,
且![]() ,
,
当![]() 时,
时,
![]() 直线
直线![]() :
:![]() ,
,
设线段![]() 的中点为
的中点为![]() ,则
,则![]() ,
,
所以![]() ,所以
,所以![]() ,
,
从而CD:![]() 即
即![]() ,
,
上述方程代入![]() 得:
得:![]() (*),
(*),
因为CD是![]() 的垂直平分线,所以线段CD是圆N的直径,
的垂直平分线,所以线段CD是圆N的直径,
所以![]() ,解得:
,解得:![]() .
.
所以直线AB:![]() .此时CD:
.此时CD:![]() ,
,![]() 时
时![]() ,
,
方程(*)化简为:![]() ,求得
,求得![]() ,
,
圆N:![]() ;
;
当![]() 时,同理求得AB:
时,同理求得AB:![]() ,圆N:
,圆N:![]() .
.
综上,直线AB:![]() ,圆N:
,圆N:![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某商场营销人员对某商品![]() 进行市场营销调查,发现每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过统计得到下表:
进行市场营销调查,发现每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过统计得到下表:
回馈点数 | 1 | 2 | 3 | 4 | 5 |
销量(百件)/天 | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)经分析发现,可用线性回归模型拟合该商品每天的销量![]() (百件)与返还点数
(百件)与返还点数![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测若回馈6个点时该商品每天销量;
,并预测若回馈6个点时该商品每天销量;
(2)已知节日期间某地拟购买该商品的消费群体十分庞大,营销调研机构对其中的200名消费者的返点数额的心理预期值进行了抽样调查,得到如下频数表:
返还点数预期值区间 |
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
(i)求这200位拟购买该商品的消费者对返点点数的心理预期值的样本平均数及中位数的估计值(同一区间的预期值可用该区间的中点值代替;估计值精确到0.1);
(ii)将对返点点数的心理预期值在![]() 和
和![]() 的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取3名进行跟踪调查,设抽出的3人中“欲望紧缩型”消费者的人数为随机变量
的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取3名进行跟踪调查,设抽出的3人中“欲望紧缩型”消费者的人数为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式及数据:①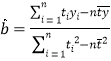 ,
,![]() ;②
;②![]() .
.