题目内容
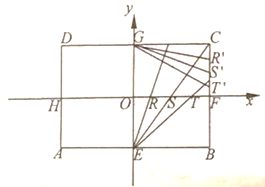
【题目】如图,矩形ABCD中,![]() ,
,![]() ,E,F,G,H分别是矩形四条边的中点,R,S,T是线段OF的四等分点,
,E,F,G,H分别是矩形四条边的中点,R,S,T是线段OF的四等分点,![]() ,
,![]() ,
,![]() 是线段CF的四等分点,分别以HF,EG为x,y轴建立直角坐标系,设ER与
是线段CF的四等分点,分别以HF,EG为x,y轴建立直角坐标系,设ER与![]() ER与
ER与![]() 分别交于
分别交于![]() ,
,![]() ,ES与
,ES与![]() ES与
ES与![]() 交于
交于![]() ,
,![]() ,ET与
,ET与![]() 交于点N,则下列关于点
交于点N,则下列关于点![]() ,
,![]() ,
,![]() ,
,![]() ,N与两个椭圆:
,N与两个椭圆:![]() :
:![]() ,
,![]() :
:![]() 的位置关系叙述正确的是( )
的位置关系叙述正确的是( )
A.三点![]() ,
,![]() ,Nspan>在
,Nspan>在![]() ,点
,点![]() 在
在![]() 上B.
上B.![]() ,
,![]() 不在
不在![]() 上,
上,![]() ,N在
,N在![]() 上
上
C.点![]() 在
在![]() 上,点
上,点![]() ,
,![]() ,
,![]() 均不在
均不在![]() 上D.
上D.![]() ,
,![]() 在
在![]() 上,
上,![]() ,
,![]() 均不在
均不在![]() 上
上
【答案】AC
【解析】
求出![]() 的坐标,证明
的坐标,证明![]() 在
在![]() 上;求出
上;求出![]() 的坐标,证明点
的坐标,证明点![]() 在
在![]() 上.即得解.
上.即得解.
由题得E(0,-3),R(1,0),所以直线ER的方程为![]() .
.
由题得G(0,3),![]() ,所以
,所以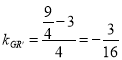 ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
联立 ,
,![]() 的坐标满足椭圆
的坐标满足椭圆![]() :
:![]() ,
,
所以![]() 在
在![]() 上.
上.
由题得ES的方程为![]() .
.
由题得![]() ,所以
,所以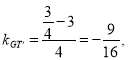
所以直线![]() 的方程为
的方程为![]() ,
,
联立直线ES和![]() 方程得
方程得![]() ,
,![]() 满足
满足![]() :
:![]() ,
,
所以点![]() 在
在![]() 上.所以选项BD错误.
上.所以选项BD错误.
由于本题属于多项选择题,所以至少两个答案正确.
故选:AC

练习册系列答案
相关题目


