题目内容
5.在平面直角坐标系xOy中,若函数y=3sin(2x+$\frac{π}{4}$)的图象向左平移φ(0<φ<$\frac{π}{2}$)个单位后,所得函数图象关于原点成中心对称,则φ的值为$\frac{3π}{8}$.分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,可得所得函数图象对应的函数解析式;再利用正弦函数的图象的对称性求得2φ+$\frac{π}{4}$=kπ,k∈z,由此求得φ的值.
解答 解:函数y=3sin(2x+$\frac{π}{4}$)的图象向左平移φ(0<φ<$\frac{π}{2}$)个单位后,所得函数图象对应的函数解析式为y=3sin(2x+2φ+$\frac{π}{4}$),
由于所得函数图象关于原点成中心对称,∴2φ+$\frac{π}{4}$=kπ,k∈z,则φ=$\frac{kπ}{2}$-$\frac{π}{8}$,k∈z.
∴φ=$\frac{3π}{8}$,
故答案为:$\frac{3π}{8}$.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知数列{an}满足2an+1+an=0,a2=1,则{an}的前9项和等于( )
| A. | -$\frac{2}{3}$(1-2-9) | B. | $\frac{1}{3}$(1-2-9) | C. | -$\frac{4}{3}$(1+2-9) | D. | (1-2-9) |
14.已知函数f(x)=sinωx(ω>0)的图象与直线y=1的相邻交点之间的距离为π,f(x)的图象向左平移$\frac{π}{6}$个单位后,得到函数y=g(x)的图象.下列关于y=g(x)的说法正确的是( )
| A. | 图象关于点$({-\frac{π}{3},0})$中心对称 | B. | 图象关于$x=-\frac{π}{6}$轴对称 | ||
| C. | 在区间$[{-\frac{5π}{12},-\frac{π}{6}}]$上单调递增 | D. | 在区间$[{-\frac{π}{6},\frac{π}{3}}]$上单调递减 |
15.甲、乙两名射手各打了10发子弹,其中甲击中环数与次数如表:
乙击中环数的概率分布如下表:
(1)若甲、乙各打一枪,球击中18环的概率及p的值;
(2)比较甲、乙射击水平的优劣.
| 环数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 次数 | 1 | 1 | 1 | 1 | 2 | 4 |
| 环数 | 7 | 8 | 9 | 10 |
| 概率 | 0.2 | 0.3 | P | 0.1 |
(2)比较甲、乙射击水平的优劣.
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴为4,离心率e=$\frac{\sqrt{3}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴为4,离心率e=$\frac{\sqrt{3}}{2}$.


 已知某地区小学生3500人,初中生4500人,高中生2000人,近视情况如图所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为200,20.
已知某地区小学生3500人,初中生4500人,高中生2000人,近视情况如图所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为200,20.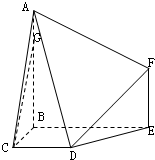 如图,在多面体ABCDEF中,BA⊥BE,BA⊥BC,BE⊥BC,AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1,G在线段AB上,且BG=3GA.
如图,在多面体ABCDEF中,BA⊥BE,BA⊥BC,BE⊥BC,AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1,G在线段AB上,且BG=3GA.