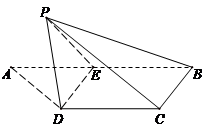题目内容
已知平面四边形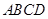 的对角线
的对角线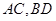 交于点
交于点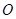 ,
,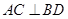 ,且
,且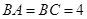 ,
,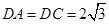 ,
,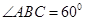 .现沿对角线
.现沿对角线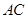 将三角形
将三角形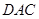 翻折,使得平面
翻折,使得平面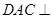 平面
平面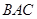 .翻折后: (Ⅰ)证明:
.翻折后: (Ⅰ)证明: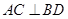 ;(Ⅱ)记
;(Ⅱ)记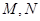 分别为
分别为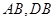 的中点.①求二面角
的中点.①求二面角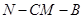 大小的余弦值; ②求点
大小的余弦值; ②求点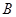 到平面
到平面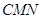 的距离
的距离
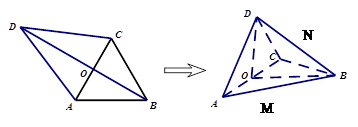
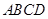 的对角线
的对角线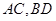 交于点
交于点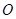 ,
,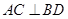 ,且
,且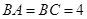 ,
,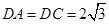 ,
,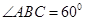 .现沿对角线
.现沿对角线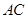 将三角形
将三角形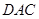 翻折,使得平面
翻折,使得平面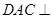 平面
平面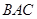 .翻折后: (Ⅰ)证明:
.翻折后: (Ⅰ)证明: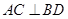 ;(Ⅱ)记
;(Ⅱ)记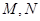 分别为
分别为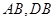 的中点.①求二面角
的中点.①求二面角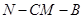 大小的余弦值; ②求点
大小的余弦值; ②求点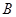 到平面
到平面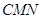 的距离
的距离 
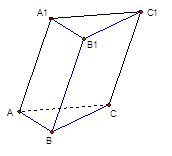
解:(Ⅰ)证明:因为平面四边形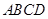 的对角线
的对角线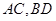 交于点
交于点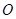 ,
,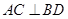 ,那么沿着AC折叠前后,垂直关系不变,因此
,那么沿着AC折叠前后,垂直关系不变,因此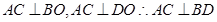
(II)分别以OD,OA,OB为z,x,y轴建立空间直角坐标系,然后表示出点的坐标,求解法向量来求解二面角和点到面的距离。因为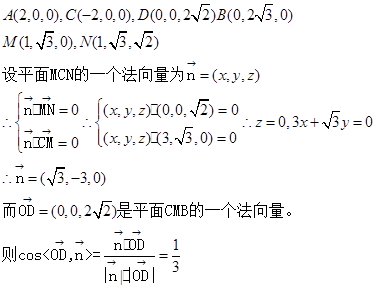
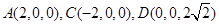
解得二面角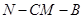 大小的余弦值为
大小的余弦值为
且有 ,而点
,而点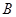 到平面
到平面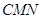 的距离为
的距离为
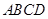 的对角线
的对角线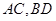 交于点
交于点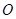 ,
,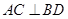 ,那么沿着AC折叠前后,垂直关系不变,因此
,那么沿着AC折叠前后,垂直关系不变,因此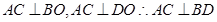
(II)分别以OD,OA,OB为z,x,y轴建立空间直角坐标系,然后表示出点的坐标,求解法向量来求解二面角和点到面的距离。因为
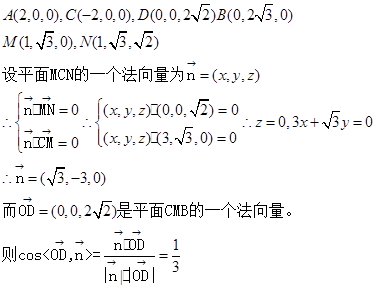
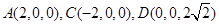
解得二面角
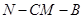 大小的余弦值为
大小的余弦值为
且有
 ,而点
,而点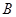 到平面
到平面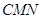 的距离为
的距离为
本试题主要考查了空间中点、线、面的位置关系的综合运用。以及线线垂直和二面角的求解的立体几何试题运用。

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 中,
中, ="2" ,
="2" ,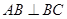 .点
.点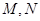 分别是
分别是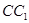 ,
,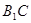 的中点,
的中点,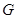 是棱
是棱 上的动点.
上的动点.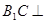 平面
平面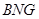 ;
;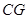 //平面
//平面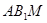 ,试确定
,试确定 的余弦值.
的余弦值.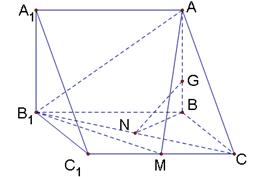 【
【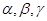 ,直线
,直线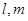 满足:
满足: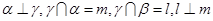 ,那么
,那么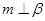 ; ②
; ②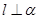 ; ③
; ③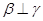 ; ④
; ④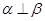 。
。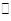 a,那么c与b的位置关系是( )
a,那么c与b的位置关系是( )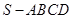 中,
中,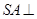 平面
平面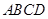 ,底面
,底面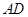 ∥
∥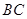 ,
,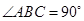 ,
,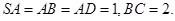
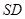 所成角的大小;
所成角的大小;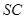 与平面
与平面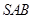 所成角的正切值;
所成角的正切值;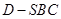 的体积.
的体积.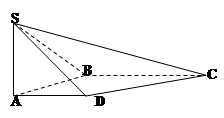
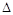 ABC
ABC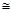
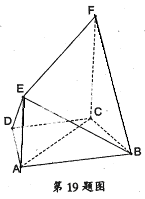
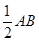 ,∠ACF=∠ADC=
,∠ACF=∠ADC=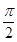 。
。
 是矩形,
是矩形,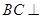 平面
平面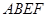 ,四边形
,四边形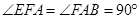 ,
,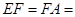
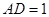 ,点
,点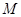 是
是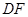 的中点,
的中点,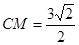 .
.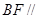 平面
平面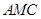 ;
;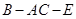 的余弦值.
的余弦值. 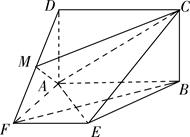
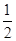 AB=a,E是AB的中点,将ΔADE沿DE折起,使点A折到点P的位置,且二面角P-DE-C的大小为120°.
AB=a,E是AB的中点,将ΔADE沿DE折起,使点A折到点P的位置,且二面角P-DE-C的大小为120°.