题目内容
如图,在三棱锥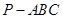 中,
中,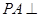 底面
底面 ,
,
点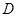 ,
,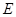 分别在棱
分别在棱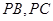 上,且
上,且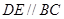
(Ⅰ)求证: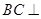 平面
平面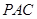 ;
;
(Ⅱ)当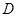 为
为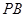 的中点时,求
的中点时,求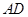 与平面
与平面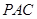 所成的角的大小;
所成的角的大小;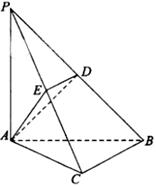
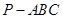 中,
中,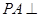 底面
底面 ,
,点
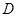 ,
,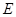 分别在棱
分别在棱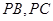 上,且
上,且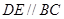
(Ⅰ)求证:
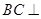 平面
平面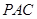 ;
;(Ⅱ)当
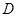 为
为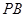 的中点时,求
的中点时,求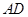 与平面
与平面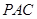 所成的角的大小;
所成的角的大小;
(1)见解析;(2)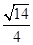
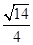
本试题主要是考查了线面垂直的证明以及二面角的求解的运用。
解:(Ⅰ)∵PA⊥底面ABC,BC?面ABC∴PA⊥BC.
又∠BCA=90°,∴AC⊥BC.
∵PA与AC相交∴BC⊥平面PAC.
(Ⅱ)∵D为PB的中点,DE∥BC,∴DE="1/" 2 BC,
又由(Ⅰ)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵PA⊥底面ABC,∴PA⊥AB,又PA=AB,
∴△ABP为等腰直角三角形,
∴AD= AB,
AB,
∴在Rt△ABC中,∠ABC=60°,
∴BC="1/" 2 AB,
∴在Rt△ADE中,sin∠DAE="DE/" AD ="BC" /2AD =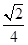 ,
,
.AD与平面PAC所成的角的余弦值为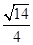 ;
;
解:(Ⅰ)∵PA⊥底面ABC,BC?面ABC∴PA⊥BC.
又∠BCA=90°,∴AC⊥BC.
∵PA与AC相交∴BC⊥平面PAC.
(Ⅱ)∵D为PB的中点,DE∥BC,∴DE="1/" 2 BC,
又由(Ⅰ)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵PA⊥底面ABC,∴PA⊥AB,又PA=AB,
∴△ABP为等腰直角三角形,
∴AD=
 AB,
AB,∴在Rt△ABC中,∠ABC=60°,
∴BC="1/" 2 AB,
∴在Rt△ADE中,sin∠DAE="DE/" AD ="BC" /2AD =
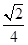 ,
,.AD与平面PAC所成的角的余弦值为
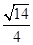 ;
; 
练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
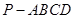 的底面
的底面 是矩形,
是矩形,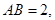
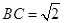 ,且侧面
,且侧面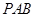 是正三角形,平面
是正三角形,平面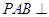 平面
平面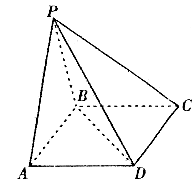
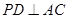 ;
;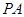 上是否存在一点
上是否存在一点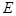 ,使得二面角
,使得二面角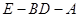 的大小为45°.若存在,试求
的大小为45°.若存在,试求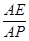 的值,若不存在,请说明理由.
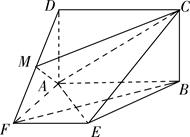
的值,若不存在,请说明理由.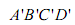 ,其中A与A '重合,且BB'<DD'<CC'.
,其中A与A '重合,且BB'<DD'<CC'.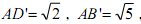 ,正方形的边长为
,正方形的边长为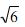 ,
, 的余弦值.
的余弦值.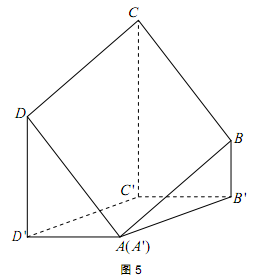
 中,
中, ="2" ,
="2" ,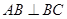 .点
.点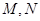 分别是
分别是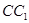 ,
,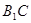 的中点,
的中点,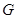 是棱
是棱 上的动点.
上的动点.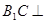 平面
平面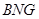 ;
;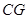 //平面
//平面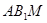 ,试确定
,试确定 的余弦值.
的余弦值.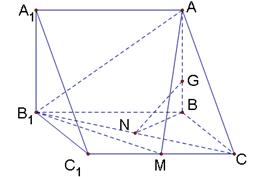 【
【 ,直线
,直线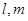 满足:
满足: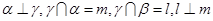 ,那么
,那么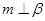 ; ②
; ②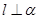 ; ③
; ③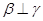 ; ④
; ④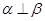 。
。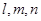 是三条不同的直线,
是三条不同的直线,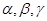 是三个不同的平面,现给出四个命题:
是三个不同的平面,现给出四个命题: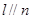 且
且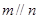 ,则
,则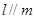 ; ②若
; ②若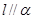 且
且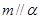 ,则
,则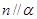 且
且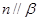 ,则
,则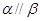 ; ④若
; ④若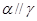 且
且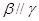 ,则
,则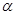 、
、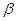 是两个不同的平面,则下列说法正确的是
是两个不同的平面,则下列说法正确的是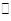 a,那么c与b的位置关系是( )
a,那么c与b的位置关系是( )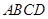 是矩形,
是矩形,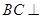 平面
平面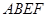 ,四边形
,四边形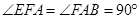 ,
,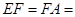
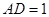 ,点
,点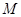 是
是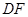 的中点,
的中点,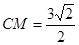 .
.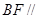 平面
平面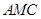 ;
;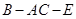 的余弦值.
的余弦值.