题目内容
已知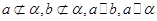 。求证:
。求证: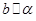 。
。
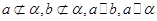 。求证:
。求证: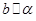 。
。证明见解析
本试题主要是考查了线面平行的判定定理的运用。
证明:过a作平面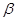 ,使它与
,使它与 相交,交线为c。
相交,交线为c。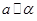 ,
, ,
,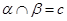 ,所以
,所以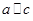 。所以
。所以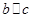 ,
,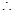
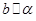 。考核综合线面平行的判定与性质。较易。
。考核综合线面平行的判定与性质。较易。
证明:过a作平面
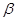 ,使它与
,使它与 相交,交线为c。
相交,交线为c。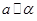 ,
, ,
,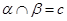 ,所以
,所以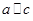 。所以
。所以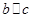 ,
,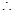
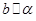 。考核综合线面平行的判定与性质。较易。
。考核综合线面平行的判定与性质。较易。
练习册系列答案
相关题目
题目内容
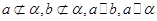 。求证:
。求证: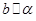 。
。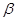 ,使它与
,使它与 相交,交线为c。
相交,交线为c。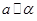 ,
, ,
,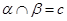 ,所以
,所以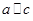 。所以
。所以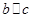 ,
,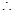
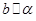 。考核综合线面平行的判定与性质。较易。
。考核综合线面平行的判定与性质。较易。