题目内容
三棱锥P-ABC中∠ABC=90°,PA=PB=PC,则下列说法正确的是
| A.平面PAC⊥平面ABC | B.平面PAB⊥平面PBC |
| C.PB⊥平面ABC | D.BC⊥平面PAB |
A
解:如图,因为∠ABC=90°,PA=PB=PC,
所以点P在底面的射影落在△ABC的斜边的中点O处,
连接OB、OP,则PO⊥OB.又∵PA=PC,所以PO⊥AC,且AC∩OB=O,
所以PO⊥平面ABC.又∵PO?平面PAC,∴平面PAC⊥平面ABC,
故选A.
所以点P在底面的射影落在△ABC的斜边的中点O处,
连接OB、OP,则PO⊥OB.又∵PA=PC,所以PO⊥AC,且AC∩OB=O,
所以PO⊥平面ABC.又∵PO?平面PAC,∴平面PAC⊥平面ABC,
故选A.

练习册系列答案
相关题目
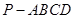 的底面
的底面 是矩形,
是矩形,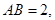
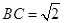 ,且侧面
,且侧面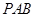 是正三角形,平面
是正三角形,平面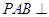 平面
平面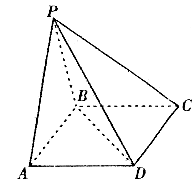
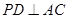 ;
;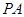 上是否存在一点
上是否存在一点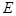 ,使得二面角
,使得二面角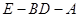 的大小为45°.若存在,试求
的大小为45°.若存在,试求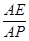 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.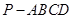 的底面是正方形,
的底面是正方形,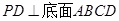 ,点E在棱PB上。
,点E在棱PB上。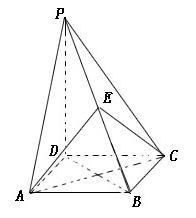
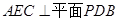 ;
;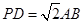 且E为PB的中点时,求AE与平
且E为PB的中点时,求AE与平 中,
中, ="2" ,
="2" ,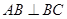 .点
.点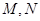 分别是
分别是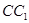 ,
,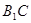 的中点,
的中点,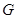 是棱
是棱 上的动点.
上的动点.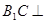 平面
平面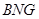 ;
;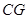 //平面
//平面 ,试确定
,试确定 的余弦值.
的余弦值.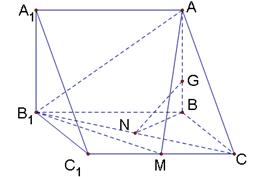 【
【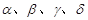 表示平面,
表示平面,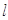 为直线,下列命题中为真命题的是 ( )
为直线,下列命题中为真命题的是 ( )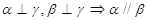
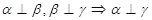
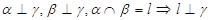
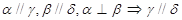
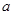 、
、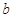 、
、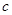 表示三条不同的直线,
表示三条不同的直线,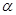 表示平面,给出下列命题:
表示平面,给出下列命题: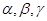 ,直线
,直线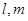 满足:
满足: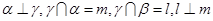 ,那么
,那么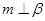 ; ②
; ②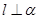 ; ③
; ③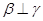 ; ④
; ④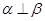 。
。