题目内容
如图,三棱锥P-ABC中,已知PA^平面ABC, PA=3,PB=PC=BC="6," 求二面角P-BC-A的正弦值

解:取BC的中点D,连结PD,AD,∵ PB =PC,∴ PD⊥BC
∵ PA⊥平面ABC,由三垂线定理的逆定理得 AD⊥BC
∴ ∠PDA就是二面角P-BC-A的平面角
∵ PB = PC = BC =" 6" ,∴ PD =

sin∠PDA=
 即二面角P-BC-A的正弦值是
即二面角P-BC-A的正弦值是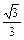


∵ PA⊥平面ABC,由三垂线定理的逆定理得 AD⊥BC

∴ ∠PDA就是二面角P-BC-A的平面角

∵ PB = PC = BC =" 6" ,∴ PD =


sin∠PDA=

 即二面角P-BC-A的正弦值是
即二面角P-BC-A的正弦值是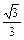

略

练习册系列答案
相关题目



 平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为
平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为 ,圆锥母线的长为
,圆锥母线的长为

 ,求所制作的圆锥形容器容积多少立方米(精确到0. 01m3) (6分)
,求所制作的圆锥形容器容积多少立方米(精确到0. 01m3) (6分) 的棱长均相等,则
的棱长均相等,则 与侧面
与侧面 所成角的正切值为 .
所成角的正切值为 .  中,其中
中,其中 ,
, 外接球球心为点O,外接球体积为
外接球球心为点O,外接球体积为 ,若
,若 的最小值为
的最小值为 ,则
,则 两点的球面距离为 .
两点的球面距离为 .
 的底面为矩形,
的底面为矩形, 且
且 平面
平面 分别为
分别为 的中点.
的中点.
 ;
; 的大小值.
的大小值. ,若
,若 ,且
,且 与
与 相交但不垂直,直线
相交但不垂直,直线 分别为
分别为 ;②任意
;②任意 ; ③存在
; ③存在 ; ④存在
; ④存在 ; ⑤任意
; ⑤任意 ; ⑥存在
; ⑥存在 。真命题的序号是_________ 。
。真命题的序号是_________ 。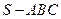 中,已知点
中,已知点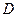 、
、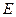 、
、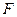 分别为棱
分别为棱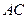 、
、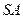 、
、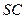 的中点.
的中点.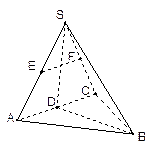
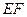 ∥平面
∥平面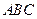 ;
; )若
)若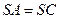 ,
,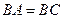 ,求证:
,求证: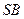 .
.