题目内容
【题目】已知函数![]() 的图像经过点
的图像经过点![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线恰好与直线
处的切线恰好与直线![]() 垂直.
垂直.
(1)求实数![]() 的值;
的值;
(2)求在函数![]() 图像上任意一点处切线的斜率的取值范围.
图像上任意一点处切线的斜率的取值范围.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:第一问根据导数的几何意义,对函数求导,求出切线的斜率,根据两条直线垂直,斜率互为负倒数,列出方程,再结合函数图象过点M,列出方程组,解方程组求出a,b,第二问把a,b的值代入函数解析式,求出导数,根据导数的几何意义,表示出切线的斜率,利用配方法求出二次函数的值域,即切线斜率的范围.
试题解析:
(1)因为y′=f′(x)=3ax2+2bx.
∵f(x)=ax3+bx2的图象过点M(1,4),
∴a+b=4.
又∵曲线在点M处的切线与直线x+9y=0垂直,
∴f′(1)=9,∴3a+2b=9.
由![]() 得,
得, ![]() .
.
(2)由(1)知y′=f′(x)=3ax2+2bx=3x2+6x
=3(x+1)2-3≥-3.

练习册系列答案
相关题目
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏。将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
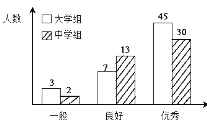
(Ⅰ)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的2×2列联表,并据此资料你是否有95﹪的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注: 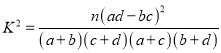 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0. 005 |
| 2.706 | 3.841 | 7.879 |
(Ⅱ)若江西参赛选手共80人,用频率估计概率,试估计其中优秀等级的选手人数;
(Ⅲ)如果在优秀等级的选手中取4名,在良好等级的选手中取2名,再从这6人中任选3人组成一个比赛团队,求所选团队中的有2名选手的等级为优秀的概率.