题目内容
【题目】已知△ABC中,A,B,C的对边分别是a,b,c,且2cos2 ![]() sinB,a=3c
sinB,a=3c
(Ⅰ)分别求tanC和sin2C的值;
(Ⅱ)若b=1,求△ABC的面积.
【答案】解:(Ⅰ)∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,即:
,即: ![]() ,
,
∴ ![]() 或
或 ![]() (舍),即
(舍),即 ![]() ,
,
∵a=3c,根据正弦定理可得:sinA=3sinC,
∵sin(B+C)=sinA,
∴ ![]() ,
,
经化简得: ![]() ,
,
∴ ![]() .
.
根据基本关系式可计算得: ![]() ,
,
∴ ![]() .
.
(Ⅱ)∵ ![]() ,
,
∴ ![]() ,
,
根据余弦定理及题设可得:  ,
,
解得: ![]() ,
,
∴ ![]()
【解析】(Ⅰ)利用三角函数恒等变换的应用化简 ![]() ,可得
,可得 ![]() ,结合B的范围即可求得
,结合B的范围即可求得 ![]() ,由a=3c,根据正弦定理,三角函数恒等变换的应用化简可得
,由a=3c,根据正弦定理,三角函数恒等变换的应用化简可得 ![]() ,根据基本关系式可计算得sinC,cosC的值,利用倍角公式即可求得sin2C的值.(Ⅱ)由
,根据基本关系式可计算得sinC,cosC的值,利用倍角公式即可求得sin2C的值.(Ⅱ)由 ![]() ,根据余弦定理及题设可解得c,a的值,利用三角形面积公式即可计算求解.
,根据余弦定理及题设可解得c,a的值,利用三角形面积公式即可计算求解.
【考点精析】通过灵活运用正弦定理的定义和余弦定理的定义,掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此题.
即可以解答此题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: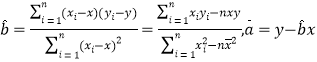 .
.