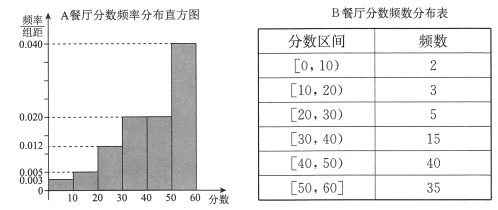
题目内容
【题目】已知函数![]() ,函数
,函数![]() ,(
,( ![]() ),若对任意
),若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,则
成立,则![]() 的取值范围是__________.
的取值范围是__________.
【答案】![]()
【解析】对函数f(x)求导可得: 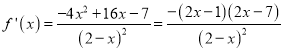 ,
,
令f′(x)=0解得![]() 或
或![]() .当x变化时,f′(x),f(x)的变化情况如下表所示:
.当x变化时,f′(x),f(x)的变化情况如下表所示:
x | 0 |
|
|
| 1 |
f′(x) |
| 0 | + |
| |
f(x) |
| 单调递减 | 4 | 单调递增 | 3 |
所以,当![]() 时,f(x)是减函数;当
时,f(x)是减函数;当![]() 时,f(x)是增函数。
时,f(x)是增函数。
当x∈[0,1]时,f(x)的值域是[4,3].
对函数g(x)求导,则g′(x)=3(x2a2).
因为a1,当x∈(0,1)时,g′(x)<3(1a2)0,
因此当x∈(0,1)时,g(x)为减函数,
从而当x∈[0,1]时有g(x)∈[g(1),g(0)],
又g(1)=12a3a2,g(0)=2a,
即当x∈[0,1]时有g(x)∈[12a3a2,2a],
任给x1∈[0,1],f(x1)∈[4,3],存在x0∈[0,1]使得g(x0)=f(x1),
则[12a3a2,2a][4,3],即![]() ,
,
解①式得a1或a![]() ,
,
解②式得a![]() ,
,
又a1,故a的取值范围内是![]() .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目