题目内容
【题目】长方形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 中点(图1).将△
中点(图1).将△![]() 沿
沿![]() 折起,使得
折起,使得![]() (图2).在图2中:
(图2).在图2中:
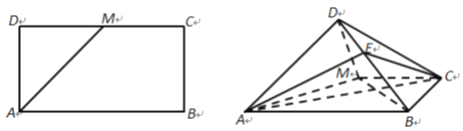
(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)![]() .
.
【解析】试题分析:
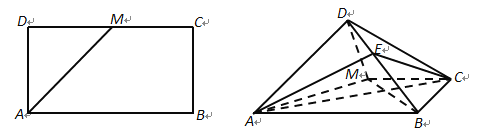
(1)要证两平面垂直,就要证线面垂直,也就要证线线垂直,由长方形![]() 的条件可得
的条件可得![]() ,再结合已知垂直,可得
,再结合已知垂直,可得![]() 平面
平面![]() ,从而可得面面垂直;
,从而可得面面垂直;
(2)由![]() 可知
可知![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离的
的距离的![]() ,而
,而![]() 到平面
到平面![]() 的距离,只要过
的距离,只要过![]() 作
作![]() 于
于![]() ,则
,则![]() 的长就是
的长就是![]() 到平面
到平面![]() 的距离,从而易求得棱锥的体积.
的距离,从而易求得棱锥的体积.
试题解析:
(1)长方形![]() 中,连结
中,连结![]() ,在因为
,在因为![]() ,
, ![]() 是
是![]() 中点,所以
中点,所以![]() ,从而
,从而![]() ,所以
,所以![]() .
.
因为![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]()
![]() 平面
平面![]() .
.
(2)设![]() 是
是![]() 中点,连结
中点,连结![]() ,则
,则![]()
![]() ,
, ![]() .
.
因为平面![]()
![]() 平面
平面![]() ,交线是
,交线是![]() ,所以
,所以![]()
![]() 平面
平面![]() .
.
因为![]() ,所以
,所以![]() 到平面
到平面![]() 距离等于
距离等于![]() .
.
因为![]() ,所以
,所以![]() ,
, ![]() ,△
,△![]() 面积为
面积为![]() .
.
所以三棱锥![]() 的体积为
的体积为![]() .
.

练习册系列答案
相关题目