Question

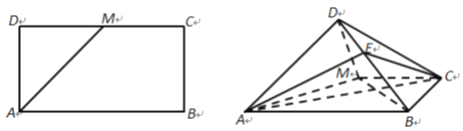
【题目】如图，底面半径为，母线长为的圆柱的轴截面是四边形，线段上的两动点， 满足.点在底面圆上，且， 为线段的中点.

(Ⅰ)求证： 平面；

(Ⅱ)四棱锥的体积是否为定值，若是，请求出该定值；若不是，请说明理由.

Answer 1

【答案】(1)见解析；（2）

【解析】试题分析：

（1）要证线面平行，考虑到Q是AP的中点，因此可再取PB的中点H，从而由中位线定理得HQ与EF平行且相等，因此有FQ//HE，从而得线面平行；

（2）P点是固定的，平面ABCD是不变的，因此四棱锥的高是定值，而四棱锥的底面ABEF的面积也是不变的，因此体积为定值，由体积公式可得体积．

试题解析：

(1)证明：设PB的中点为F，连接HE，HQ，

在△ABP中，利用三角形中位线的性质可得QH∥AB，且QH＝AB，

又EF∥AB，EF＝AB，所以EF∥HQ，EF＝HQ，

所以四边形EFQH为平行四边形，所以FQ∥HE，

所以FQ∥平面BPE.

(2)四棱锥PABEF的体积为定值，定值为.理由如下：

由已知可得梯形ABEF的高为2，所以S梯形ABEF＝×2＝3，

又平面ABCD⊥平面ABP，过点P向AB作垂线PG，垂足为G，

则由面面垂直的性质定理可得PG⊥平面ABCD，

又AP＝，AB＝2，∠APB＝90°，所以BP＝1，

所以PG＝＝，所以V四棱锥PABEF＝×PG×S梯形ABEF＝××3＝，

所以四棱锥PABEF的体积为定值，定值为