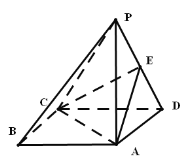
题目内容
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,左焦点
,左焦点![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点, ![]() 为椭圆上异于
为椭圆上异于![]() 的点.
的点.
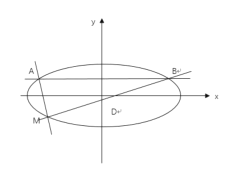
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 过
过![]() 点,求圆
点,求圆![]() 的标准方程;
的标准方程;
(3)设直线![]() 与
与![]() 轴分别交于
轴分别交于![]() ,证明:
,证明: ![]() 为定值.
为定值.
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1)根据离心率为![]() ,左焦点
,左焦点![]() ,可求出
,可求出![]() 和
和![]() ,从而求出椭圆
,从而求出椭圆![]() 的方程;(2)设
的方程;(2)设![]() ,则
,则![]() ,且
,且![]() ,由
,由![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 过
过![]() 点可得
点可得![]() 即
即![]() ,从而可求出圆
,从而可求出圆![]() 的标准方程;(3)设
的标准方程;(3)设![]() ,则
,则![]() 的方程为
的方程为![]() ,求出
,求出![]() 两点的纵坐标,则
两点的纵坐标,则![]()
![]() ,化简求得.
,化简求得.
试题解析:(1)∵![]() 且
且![]()
∴![]() ,
, ![]() .
.
∴椭圆方程为![]() .
.
(2)设![]() ,则
,则![]() ,且
,且![]() .①
.①
∵以![]() 为直径的圆
为直径的圆![]() 过
过![]() 点
点
∴![]()
∴![]() ,
,
又∵![]() ,
, ![]()
∴![]() .②
.②
由①②解得: ![]() ,或
,或![]() (舍)
(舍)
∴![]() .
.
又∵圆![]() 的圆心为
的圆心为![]() 的中点
的中点![]() ,半径为
,半径为![]() ,
,
∴圆![]() 的标准方程为
的标准方程为![]() .
.
(3)设![]() ,则
,则![]() 的方程为
的方程为![]() ,若
,若![]() 不存在,显然不符合条件.
不存在,显然不符合条件.
令![]() 得
得![]() ;同理
;同理![]() ,
,
∴![]()
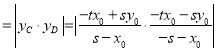
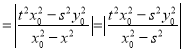
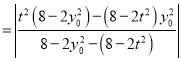
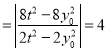 为定值.
为定值.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案【题目】2017年交警统计了某路段过往车辆的车速大小与发生交通事故的次数,得到如表所示的数据:
车速x(km/h) | 60 | 70 | 80 | 90 | 100 |
事故次数y | 1 | 3 | 6 | 9 | 11 |
(1)请画出上表数据的散点图;

(2)请根据上表提供的数据,求出y关于x的线性回归方程![]() =
=![]() x+
x+![]() ;
;
(3)根据(2)所得速度与事故发生次数的规律,试说明交管部门可采取什么措施以减少事故的发生.
附:![]() =
=![]() ,
,![]() =
=![]() -
-![]()
【题目】一研究性学习小组对春季昼夜温差大小与某大豆种子发芽多少之间的关系进行分析研究,他们分别记录了4月1日至4月5日的每天昼夜温差与实验室每天每100颗种子的发芽数,得到如下数据:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
温差 | 8 | 12 | 13 | 11 | 10 |
发芽数 | 18 | 26 | 30 | 25 | 20 |
该学习组所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再用被选取的2组数据进行检验.
(1)求选取的2组数据恰好是相邻2天的数据的概率;
(2)若选取的是4月1日与4月5日这2组数据做检验,请根据4月2日至4月4日这3组数据求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)所得的线性回归方程是否可靠?
参考公式和数据: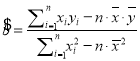 ,
,![]() ;
;![]() ,
,![]()