题目内容
【题目】(1)数列{an}的前n项和为Sn=10n﹣n2,求数列{|an|}的前n项和.
(2)已知等差数列{an}满足a2=0,a6+a8=﹣10.求数列{![]() }的前n项和.
}的前n项和.
【答案】(1)Tn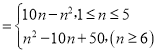 ;(2)Hn
;(2)Hn![]() .
.
【解析】
(1)根据Sn=10n﹣n2,利用通项与前n项和的关系,n≥2时,an=Sn﹣Sn﹣1,(n=1时也成立)求得an.令an≥0,解得n≤5.可得n≤5时,{|an|}的前n项和Tn=a1+a2+……+an=Sn.n≥6时,{|an|}的前n项和Tn=a1+a2+……a5﹣a6+……﹣an=2S5﹣Sn.即可得出Tn.
(2)设等差数列{an}的公差为d,由a2=0,a6+a8=﹣10.可得a1+d=0,2a1+12d=﹣10,联立解得:a1,d,可得an.于是![]() .利用错位相减法即可得出.
.利用错位相减法即可得出.
(1)∵Sn=10n﹣n2,
∴n≥2时,an=Sn﹣Sn﹣1=10n﹣n2﹣[10(n﹣1)﹣(n﹣1)2]=11﹣2n,
当n=1时,![]() 满足上式,故an=11﹣2n.
满足上式,故an=11﹣2n.
令an≥0,解得n≤5.
∴n≤5时,{|an|}的前n项和Tn=a1+a2+……+an=Sn=10n﹣n2.
n≥6时,{|an|}的前n项和Tn=a1+a2+……a5﹣a6+……﹣an=2S5﹣Sn=2×(50﹣25)﹣(10n﹣n2)=n2﹣10n+50.
综上可得:Tn .
.
(2)设等差数列{an}的公差为d,∵a2=0,a6+a8=﹣10.
∴a1+d=0,2a1+12d=﹣10,
联立解得:a1=1,d=﹣1,
∴an=1﹣(n﹣1)=2﹣n.
∴![]() .
.
∴数列{![]() }的前n项和Hn=1+0
}的前n项和Hn=1+0![]() .
.
![]() Hn
Hn![]() 0
0![]() .
.
相减可得:![]() Hn=
Hn=![]() ,
,
![]() ,
,
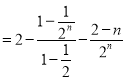
![]() .
.
![]() .
.

练习册系列答案
相关题目