题目内容
17.如图是某市4月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,记5分,空气质量指数大于200表示空气重度污染记1分,空气质量指数在100和200之间(含100和200)表示中度污染,记3分.某调查机构随机选择4月1日至4月14日中的某三天抽样评估,则该市评估得分超过10分的可能抽样情况有252种.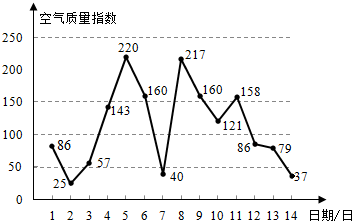
分析 有图可知,5分的有7天,1分的有2天,3分的有5天,调查机构随机选择4月1日至4月14日中的某三天抽样评估,则该市评估得分超过10分,因为5+5+1=11,5+5+3=13,5+3+3=11,5+5+5=15,故分四类,根据分类计数原理得以解决.
解答 解:有图可知,空气质量指数小于100表示空气质量优良,记5分,有7天,空气质量指数大于200表示空气重度污染记1分,有2天,空气质量指数在100和200之间(含100和200)表示中度污染,记3分,有5天,调查机构随机选择4月1日至4月14日中的某三天抽样评估,则该市评估得分超过10分,
因为5+5+1=11,5+5+3=13,5+3+3=11,5+5+5=15,
故分四类,第一类,得分为(5,5,1),有C72C21=42种,
第二类,得分为(5,5,3),有C72C51=105种,
第三类,得分为(5,3,3),有C71C52=70种,
第四类,得分为(5,5,5),有C73=35种,
根据分类计数原理,得共有42+105+70+35=252种,
故答案为:252.
点评 本题考查了分类计数原理,关键是分类.

练习册系列答案
相关题目
5.已知等比数列{an}前n项和为Sn,且a2015=3S2014+2015,a2014=3S2013+2015,则公比q等于( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | 4 | D. | $\frac{1}{4}$ |
2.在3x+2y<6表示的平面区域内的一个点是( )
| A. | (3,0) | B. | (1,3) | C. | (0,3) | D. | (0,0) |
9.已知f(x)=3sinx-πx,对任意的x∈(0,$\frac{π}{2}$),给出以下四个结论:
①f′(x)>0;
②f′(x)<0;
③f(x)>0;
④f(x)<0.
其中正确的是( )
①f′(x)>0;
②f′(x)<0;
③f(x)>0;
④f(x)<0.
其中正确的是( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
6.已知a、b、c分别为△ABC三个内角A,B,C的对边,若A=$\frac{π}{3}$,则a(cosC+$\sqrt{3}$sinC)=( )
| A. | a+b | B. | b+c | C. | a+c | D. | a+b+c |