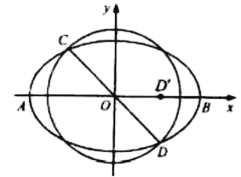
题目内容
【题目】已知函数![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数
垂直,求实数![]() 的取值;
的取值;
(Ⅱ)求函数![]() 的单调区间;
的单调区间;
(Ⅲ)记![]() .当
.当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有两个零点,求实数
上有两个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)当
;(Ⅱ)当![]() 时, 减区间为
时, 减区间为![]() ;当
;当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(1)先求出函数f(x)的定义域和导函数f′(x),再由两直线垂直的条件可得f′(1)=﹣3,求出a的值;
(2)求出f′(x),对a讨论,由f′(x)>0和f′(x)<0进行求解,即判断出函数的单调区间;
(3)由(1)和题意求出g(x)的解析式,求出g′(x),由g′(x)>0和g′(x)<0进行求解,即判断出函数的单调区间,再由条件和函数零点的几何意义列出不等式组,求出b的范围.
(Ⅰ)定义域![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
(Ⅱ)![]()
当![]() ,
,![]() ,单减区间为
,单减区间为![]()
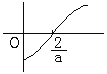
当![]() 时
时
令![]() ,单增区间为
,单增区间为![]() ;令
;令![]() ,单减区间为
,单减区间为![]()
当![]() 时,单减区间
时,单减区间![]()
∴当![]() 时, 减区间为
时, 减区间为![]() ;
;
当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;
;
(Ⅲ)![]()
![]()
![]()
令![]() ,
,![]() ,
,![]()
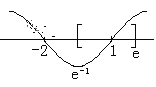
令![]() ,
,![]() ;令
;令![]() ,
,![]()
∴![]() 是
是![]() 在
在![]() 上唯一的极小值点,也是唯一的最小值点
上唯一的极小值点,也是唯一的最小值点
∴![]()
∵![]() 在
在![]() 上有两个零点
上有两个零点
∴只须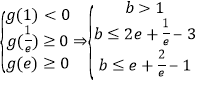
∴![]() .
.

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案【题目】某产品的三个质量指标分别为x, y, z, 用综合指标S =" x" + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(1) 用产品编号列出所有可能的结果;
(2) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
【题目】某体育老师随机调查了100名同学,询问他们最喜欢的球类运动,统计数据如表所示.已知最喜欢足球的人数等于最喜欢排球和最喜欢羽毛球的人数之和.
最喜欢的球类运动 | 足球 | 篮球 | 排球 | 乒乓球 | 羽毛球 | 网球 |
人数 | a | 20 | 10 | 15 | b | 5 |
(1)求![]() 的值;
的值;
(2)将足球、篮球、排球统称为“大球”,将乒乓球、羽毛球、网球统称为“小球”.现按照喜欢大、小球的人数用分层抽样的方式从调查的同学中抽取5人,再从这5人中任选2人,求这2人中至少有一人喜欢小球的概率.