题目内容
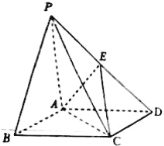
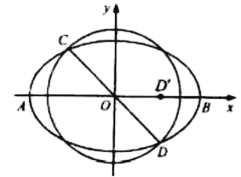
【题目】如图，已知AB为椭圆E：
（a＞b＞0）的长轴，过坐标原点O且倾斜角为135°的直线交椭圆E于C，D两点，且D在x轴上的射影D'恰为椭圆E的长半轴OB的中点．
（1）求椭圆E的离心率；
（2）若AB＝8，不过第四象限的直线l与椭圆E和以CD为直径的圆均相切，求直线l的方程．
【答案】（1）
（2）
【解析】
(1) CD的方程为y = -x因为D在x轴上的射影
恰恰为椭圆E的长半轴OB的中点，所以
，代入椭圆方程得到
进而得到离心率；（2）因为AB = 8，所以2a = 8，即a = 4.由（1）知，
从而得到圆和椭圆的方程，直线l与以CD为直径的圆相切，所以
，即
，联立直线l和椭圆E的方程组，并消去y整理得：
，因为直线l与椭圆E相切，所以，
，化简得，
解出参数值即可.
（1）因为直线CD过原点O且倾斜角为135°，
所以CD的方程为y = -x.
因为D在x轴上的射影恰恰为椭圆E的长半轴OB的中点，
所以.
代入椭圆E：
得，.
所以椭圆E的离心率
.
（2）因为AB = 8，所以2a = 8，即a = 4.由（1）知，.
从而椭圆E：
，以CD为直径的圆：
.
设直线l的方程为：
.
因为直线l与以CD为直径的圆相切，所以，即. ①
联立直线l和椭圆E的方程组，并消去y整理得：.
因为直线l与椭圆E相切，所以，.
化简得，. ②
由①②得，
，
，所以直线l的方程为.
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案【题目】某电子科技公司由于产品采用最新技术，销售额不断增长，最近
个季度的销售额数据统计如下表（其中
表示
年第一季度，以此类推）：
季度 |
|
|
|
|
|
季度编号x |
|
|
|
|
|
销售额y（百万元） |
|
|
|
|
|
（1）公司市场部从中任选
个季度的数据进行对比分析，求这个季度的销售额都超过
千万元的概率；
（2）求
关于
的线性回归方程，并预测该公司
的销售额.
附：线性回归方程：
其中
，
参考数据：
.
【题目】某小型企业甲产品生产的投入成本x（单位：万元）与产品销售收入y（单位：万元）存在较好的线性关系，下表记录了最近5次该产品的相关数据.
x（万元） | 3 | 5 | 7 | 9 | 11 |
y（万元） | 8 | 10 | 13 | 17 | 22 |
（1）求y关于x的线性回归方程；
（2）根据（1）中的回归方程，判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大（毛利率
）？
相关公式：
，
.
