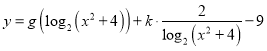题目内容
【题目】已知函数f(x)=2a·4x-2x-1.
(1)当a=1时,解不等式f(x)>0;
(2)当a=![]() ,x∈[0,2]时,求f(x)的值域.
,x∈[0,2]时,求f(x)的值域.
【答案】(1)(0,+∞);(2)[-1,11].
【解析】
(1)将a=1代入,求出函数的解析式,将2x看作一个整体,根据二次不等式的解法,求出2x的范围,结合指数函数的图象和性质,可得答案.
(2)将a=![]() 代入,求出函数的解析式,利用换元法,将问题转化为二次函数在定区间上的最值问题,求出函数最值后,得到函数的值域.
代入,求出函数的解析式,利用换元法,将问题转化为二次函数在定区间上的最值问题,求出函数最值后,得到函数的值域.
(1)当a=1时,f(x)=2·4x-2x-1.
f(x)>0,即2·(2x)2-2x-1>0,
解得2x>1或2x<-![]() (舍去),
(舍去),
∴x>0,∴不等式f(x)>0的解集为(0,+∞).
(2)当a=![]() 时,f(x)=4x-2x-1,x∈[0,2].
时,f(x)=4x-2x-1,x∈[0,2].
设t=2x.∵x∈[0,2],∴t∈[1,4].
∴y=g(t)=t2-t-1 (1≤t≤4).
画出g(t)=t2-t-1 (1≤t≤4)的图像(如图),
可知g(t)min=g(1)=-1,g(t)max=g(4)=11,
∴f(x)的值域为[-1,11].


练习册系列答案
相关题目