Question

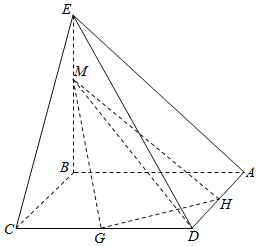
【题目】如图所示，EB垂直于菱形ABCD所在平面，且EB=BC=2，∠BAD=60°，点G、H分别为边CD、DA的中点，点M是线段BE上的动点．

（I）求证：GH⊥DM；

（II）当三棱锥D-MGH的体积最大时，求点A到面MGH的距离．

Answer 1

【答案】（Ⅰ）见解析；（II）

【解析】

（Ⅰ）先证明GH⊥平面BDE．再证明GH⊥DM；（II）先证明BM⊥平面ABCD，再计算得到．所以当点M与点E重合时，BM取得最大值2，此时（VD-MGH）max．

再求A到平面MGH的距离为.

（Ⅰ）证明：连接AC、BD相交于点O．

∵BE⊥平面ABCD．而AC平面ABCD，∴BE⊥AC．

又∵四边形ABCD为菱形，∴BD⊥AC．

∵BD∩BE=B，∴AC⊥平面BDE．

∵G、H分别为DC、AD的中点，∴GH∥AC，则GH⊥平面BDE．

而DM平面BDE，∴GH⊥DM；

（II）菱形ABCD中，∠BAD=60°，得，∠ADC=120°．

∵DG=DH=1，

∴S△DGH==，

∵BE⊥平面ABCD，即BM⊥平面ABCD，

∴=．

显然，当点M与点E重合时，BM取得最大值2，此时（VD-MGH）max=．

且MG=MH=，GH=，则，

∵H是AD中点，所以A到平面MGH的距离d1等于到平面MGH的距离d2，

又VD-MGH=VM-DGH，∴，得d2=．

∴A到平面MGH的距离为．