��Ŀ����
����Ŀ���¹�������ѧ�ҵ�����������ѧ����ɾ�����,���������ĺ��� ����Ϊ����������,����RΪʵ����,QΪ��������,����������ȷ�ĸ�����( )
����Ϊ����������,����RΪʵ����,QΪ��������,����������ȷ�ĸ�����( )
����������ڵ���������f(x)���������:
�ٶ��������x��R,����f(f(x))=1;
�ں���f(x)ż����;
�ۺ���f(x)��ֵ����{0,1};
����T��0��T������,��f(x+T)=f(x)�������x��R�����;
����f(x)ͼ���ϴ��ڲ�ͬ��������A,B,C,ʹ�á�ABCΪ�ȱ߽���.
A.2B.3C.4D.5
���𰸡�D
��������
�ٷ�![]() ��
��![]() ����������ڵ��⣬����
����������ڵ��⣬����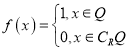 ��ֵ�ж�.�ڷ�
��ֵ�ж�.�ڷ�![]() ��
��![]() ���������������ż�Զ����ж�.�۵�
���������������ż�Զ����ж�.�۵�![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() �ж�.�ܷ�
�ж�.�ܷ�![]() ��
��![]() ����������������ں����Ķ����ж�.��ȡ
����������������ں����Ķ����ж�.��ȡ![]() ��
��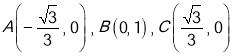 �ж�.
�ж�.
�ٵ�![]() ʱ��
ʱ��![]() ����
����![]() ����
����![]() ʱ��
ʱ��![]() ����
����![]() �����Զ��������x��R������f(f(x))=1;����ȷ.
�����Զ��������x��R������f(f(x))=1;����ȷ.
�ڵ�![]() ʱ��
ʱ��![]() ��
��![]() ����
����![]() ʱ��
ʱ��![]() ��
��![]() �����Ժ���f(x)ż����;����ȷ.
�����Ժ���f(x)ż����;����ȷ.
�۵�![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() �����Ժ���f(x)��ֵ����{0��1};����ȷ.
�����Ժ���f(x)��ֵ����{0��1};����ȷ.
�ܵ�![]() ʱ����ΪT��0��TΪ������������
ʱ����ΪT��0��TΪ������������![]() ����f(x+T)=1=f(x)����
����f(x+T)=1=f(x)���� ![]() ʱ����ΪT��0��TΪ������������
ʱ����ΪT��0��TΪ������������![]() ����f(x+T)=0=f(x)�����Զ������x��R�����;����ȷ.
����f(x+T)=0=f(x)�����Զ������x��R�����;����ȷ.
��ȡ![]() ��
��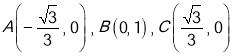 ������
������![]() Ϊ�߳��ĵȱ������Σ�����ȷ.
Ϊ�߳��ĵȱ������Σ�����ȷ.
��ѡ��D

����Ŀ������¹ڷ������飬�����й������������ҹ������Ĵ����ٶ���졢��Ⱦ��Χ��㡢�����Ѷ�����һ���ش�ͻ�����������¼�.�л�������ʷ�Ͼ������ܶ�ĥ�ѣ�������û�б�ѹ����������������£�������ĥ���гɳ�����ĥ���з���.����������У�ȫ������չ�ֳ��������ε���֮�¡����п�ѧ����֮��.ijУ����ѧ��Ҳչ���˶����������о���һ��ͬѧ������ͳ���з��֣���2020��2��1����2��7���ڼ䣬����![]() ��ȫ���ۼƱ���ȷ�ﲡ������
��ȫ���ۼƱ���ȷ�ﲡ������![]() ����λ�����ˣ�֮��Ĺ�ϵ���±���
����λ�����ˣ�֮��Ĺ�ϵ���±���
���� | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
ȫ���ۼƱ���ȷ�ﲡ������ | 1.4 | 1.7 | 2.0 | 2.4 | 2.8 | 3.1 | 3.5 |
��1�����ݱ��е����ݣ��������ϵ�����з���˵�����Ƿ���������Իع�ģ�����![]() ��
��![]() �Ĺ�ϵ��
�Ĺ�ϵ��
��2�����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��ϵ����ȷ��0.01��.��Ԥ��2��10��ȫ���ۼƱ���ȷ�ﲡ����.
��ϵ����ȷ��0.01��.��Ԥ��2��10��ȫ���ۼƱ���ȷ�ﲡ����.
�ο����ݣ�![]() ��
��![]() ��
�� ��
��![]() .
.
�ο���ʽ�����ϵ��
�ع鷽��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
 ��
��![]() .
.