题目内容
【题目】已知函数![]() ,
,![]() ,且函数
,且函数![]() 是偶函数.
是偶函数.
(1)求![]() 的解析式;
的解析式;
(2)若不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(3)若函数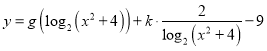 恰好有三个零点,求
恰好有三个零点,求![]() 的值及该函数的零点.
的值及该函数的零点.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() ,零点为0,-2,2
,零点为0,-2,2
【解析】
(1)由![]() 是偶函数,求出
是偶函数,求出![]() 后可得
后可得![]() ;
;
(2)等式![]() 在
在![]() 上恒成立,可用分离参数法转化为求函数最值;
上恒成立,可用分离参数法转化为求函数最值;
(3)可换元![]() ,
, 化为关于
化为关于![]() (
(![]() )的方程,原函数有三个零点,即原方程有三个解,由对称性(或偶函数)知
)的方程,原函数有三个零点,即原方程有三个解,由对称性(或偶函数)知![]() 是一个解,即
是一个解,即![]() 是新方程的一个根,由此可求得
是新方程的一个根,由此可求得![]() ,从而求得另外的根,即求得函数的零点.
,从而求得另外的根,即求得函数的零点.
(1)∵![]() ,
,
∴![]() .
.
∵![]() 是偶函数,∴
是偶函数,∴![]() ,∴
,∴![]() .∴
.∴![]() ,∴
,∴![]() .
.
(2)∵![]() 在
在![]() 上恒成立,∴
上恒成立,∴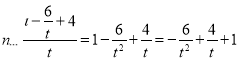 .
.
令![]() ,
,![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() .
.
(3)令![]() ,则
,则![]() ,方程
,方程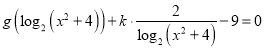 可化为
可化为![]() ,即
,即![]() ,也即
,也即![]() .
.
又∵方程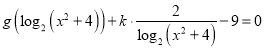 有三个实数根,
有三个实数根,
∴![]() 有一个根为2,∴
有一个根为2,∴![]() .∴
.∴![]() ,解得
,解得![]() 或
或![]() .
.
由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,
,
∴该函数的零点为0,-2,2.

练习册系列答案
相关题目