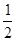题目内容
已知函数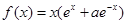 ,
,
(1)当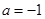 时,判断并证明
时,判断并证明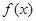 的奇偶性;
的奇偶性;
(2)是否存在实数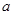 ,使得
,使得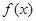 是奇函数?若存在,求出
是奇函数?若存在,求出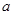 ;若不存在,说明理由。
;若不存在,说明理由。
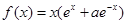 ,
,(1)当
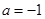 时,判断并证明
时,判断并证明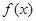 的奇偶性;
的奇偶性;(2)是否存在实数
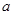 ,使得
,使得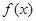 是奇函数?若存在,求出
是奇函数?若存在,求出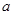 ;若不存在,说明理由。
;若不存在,说明理由。(1)偶函数;(2)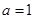
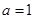
试题分析:(1)定义法判断函数奇偶性是常用的方法,定义域区间关于原点对称的函数
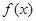 ,若
,若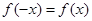 ,则
,则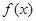 为偶函数,若
为偶函数,若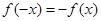 ,则函数
,则函数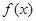 为奇函数;(2)f(x)是R奇函数,则
为奇函数;(2)f(x)是R奇函数,则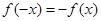 对任意x∈R恒成立.
对任意x∈R恒成立.试题解析:(1)
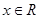 ,当
,当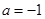 时,
时,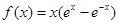 , 3分
, 3分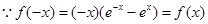 , ∴f(x)是偶函数。 6分
, ∴f(x)是偶函数。 6分(2)假设存在实数a使得f(x)是奇函数,
∵
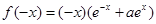 ,
,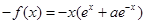 ,
,要使
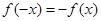 对任意x∈R恒成立,即
对任意x∈R恒成立,即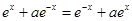 恒成立, 9分
恒成立, 9分有
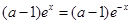 ,即
,即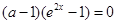 恒成立, 12分
恒成立, 12分∴
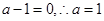 . 14分
. 14分
练习册系列答案
相关题目
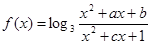 ,是否存在实数a、b、c,使
,是否存在实数a、b、c,使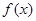 同时满足下列三个条件:(1)定义域为R的奇函数;(2)在
同时满足下列三个条件:(1)定义域为R的奇函数;(2)在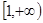 上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由.
上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由.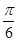 ),若存在α∈(0,π),使f(α+x)= f(α-x)对一切实数x恒成立,则α= .
),若存在α∈(0,π),使f(α+x)= f(α-x)对一切实数x恒成立,则α= . 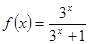 ,正项等比数列
,正项等比数列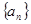 满足
满足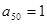 ,则
,则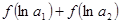
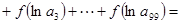 .
.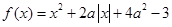 的零点有且只有一个,则实数
的零点有且只有一个,则实数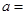 .
.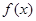 是
是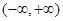 上的偶函数,若对于
上的偶函数,若对于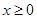 ,都有
,都有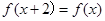 ,且当
,且当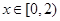 时,
时,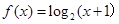 ,则
,则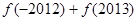 =____________.
=____________.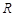 上的函数
上的函数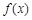 ,对任意
,对任意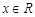 都有
都有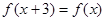 ,当
,当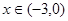 时,
时,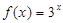 ,则
,则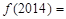 .
.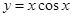 ②
② ③
③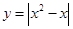 ④
④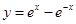 ,其中是奇函数的是( )
,其中是奇函数的是( )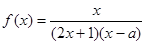 为奇函数,则
为奇函数,则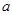 的值为 ( )
的值为 ( )