题目内容
11.已知函数f(x)=$\frac{a-{2}^{x}}{1+{2}^{x}}$(a∈R),且x∈R时,总有f(-x)=-f(x)成立.(1)求a的值;
(2)判断并证明函数f(x)的单调性;
(3)求f(x)在[0,2]上的值域.
分析 (1)根据条件建立方程关系即可求a的值;
(2)根据函数单调性的定义判断并证明函数f(x)的单调性;
(3)结合函数奇偶性和单调性的定义即可求f(x)在[0,2]上的值域.
解答 解:(1)∵f(-x)=-f(x),
∴$\frac{a-{2}^{-x}}{1+{2}^{-x}}$=-$\frac{a-{2}^{x}}{1+{2}^{x}}$,
即 $\frac{a•{2}^{x}-1}{1+{2}^{x}}$=$\frac{{2}^{x}-a}{1+{2}^{x}}$,
∴a=1,
∴f(x)=$\frac{1-{2}^{x}}{1+{2}^{x}}$.
(2)函数f(x)为 R 上的减函数,
∵f(x)的定义域为 R,
∴任取x 1,x 2∈R,且x 2>x 1,
∴f(x 2)-f(x 1)=$\frac{1-{2}^{{x}_{2}}}{1+{2}^{{x}_{2}}}$$-\frac{1-{2}^{{x}_{1}}}{1+{2}^{{x}_{1}}}$=$\frac{2({2}^{{x}_{1}}-{2}^{{x}_{2}})}{(1+{2}^{{x}_{1}})(1+{2}^{{x}_{2}})}$
∵x 2>x 1,∴${2}^{{x}_{2}}$$>{2}^{{x}_{2}}$>0.
∴f(x 2)-f(x 1)<0即f(x 2)<f(x 1).
∴函数f(x)为 R 上的减函数.----(11分)
(3)由(2)知,函数f(x)在[0,2]上的为减函数,
∴f(2)≤f(x)≤f(0),
即-$\frac{3}{5}$≤f(x)≤0,
即函数的值域为[-$\frac{3}{5}$,0]----------(14分)
点评 本题主要考查函数奇偶性的应用以及函数单调性和值域的求解,利用定义法是解决本题的关键.

| A. | f(g(a-1))>f(g(a)) | B. | f(g($\frac{2a}{3}$))>f(g($\frac{5a}{3}$)) | ||
| C. | g(f($\frac{{4}^{n}+1}{{4}^{n}-1}$))>g(f(3))(其中a≠0且a$≠\frac{1}{2}$) | D. | g(f($\frac{{2}^{n}+1}{{2}^{n}-1}$))>g(f(3))(其中a≠0,且a≠1) |
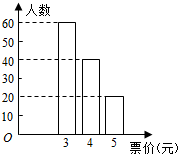 2014 年12 月28 日开始,北京市公共电汽车和地铁按照里程分段计价.具体如下表.(不考虑公交卡折扣情况)
2014 年12 月28 日开始,北京市公共电汽车和地铁按照里程分段计价.具体如下表.(不考虑公交卡折扣情况)| 乘公共汽车方案 | 10公里(含)内2元; 10公里以上部分,每增加1元可乘坐5公里(含) |
| 乘坐地铁方案(不含机场线) | 6公里(含)内3元 6公里至12公里(含)4元 12公里至22公里(含)5元 |
| 22公里至32公里(含)6元 32公里以上部分,每增加1元可乘坐20公里(含) |
(Ⅰ)如果从那些只乘坐四号线地铁,且在陶然亭站出站的乘客中任选1 人,试估计此人乘坐地铁的票价小于5 元的概率;
(Ⅱ)从那些只乘坐四号线地铁,且在陶然亭站出站的乘客中随机选2 人,记x 为这2人乘坐地铁的票价和,根据统计图,并以频率作为概率,求X 的分布列和数学期望;
(Ⅲ)小李乘坐地铁从A 地到陶然亭的票价是5 元,返程时,小李乘坐某路公共电汽车所花交通费也是5 元,假设小李往返过程中乘坐地铁和公共电汽车的路程均为s 公里,试写出s 的取值范围.(只需写出结论)
| 流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
| 人数 | 1 | 6 | 6 | 5 | 2 | 0 |
(2)估计此地1000名使用4G手机用户中每日使用流量不少于10M用户数;
(3)在15≤x<20和20≤x<25两组用户中,随机抽取两人作进一步问卷调查,求所抽取的两人恰好来自不同组的概率.