Question

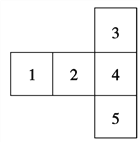
【题目】编号为A，B，C，D，E的5个小球放在如图所示的5个盒子里，要求每个盒子只能放1个小球，且A球不能放在1，2号盒子里，B球必须放在与A球相邻的盒子中，求不同的放法有多少种？

Answer 1

【答案】．

【解析】试题分析：借助题设条件运用排列数组合数公式和分类计数原理求解．

试题解析:

根据A球所在位置分三类：

（1）若A球放在3号盒子内，则B球只能放在4号盒子内，余下的三个盒子放球C、D、E，则根据分步计数原理得，此时有A＝6种不同的放法；

（2）若A球放在5号盒子内，则B球只能放在4号盒子内，余下的三个盒子放球C、D、E，则根据分步计数原理得，此时有A＝6种不同的放法；

（3）若A球放在4号盒子内，则B球可以放在2号、3号、5号盒子中的任何一个，余下的三个盒子放球C、D、E，有A＝6种不同的放法，根据分步计数原理得，此时有AA＝18种不同的放法．

综上所述，由分类计数原理得不同的放法共有6＋6＋18＝30种．