题目内容
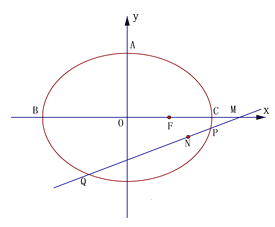
【题目】在直角坐标系xOy中,直线l过点P (3, ![]() )且倾斜角为
)且倾斜角为![]() .在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
.在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为![]() .
.
(Ⅰ)求直线l的一个参数方程和圆C的直角坐标方程;
(Ⅱ)设圆C与直线l交于点A,B,求![]() 的值.
的值.
(2)已知函数![]() .
.
(Ⅰ)求函数![]() 的最小值
的最小值![]() ;
;
(Ⅱ)若正实数![]() 满足
满足![]() ,且
,且![]() 对任意的正实数
对任意的正实数![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)(Ⅰ)直线l参数方程为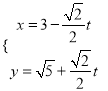 (t为参数),圆C的直角坐标方程为x2+(y-
(t为参数),圆C的直角坐标方程为x2+(y-![]() )2=5 (Ⅱ)|PA||PB|=|t1t2|=4(2)(Ⅰ)1(Ⅱ)
)2=5 (Ⅱ)|PA||PB|=|t1t2|=4(2)(Ⅰ)1(Ⅱ)![]()
【解析】试题分析:
(1)(Ⅰ)利用转化关系可得直线l参数方程为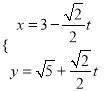 (t为参数) ,圆的直角坐标方程为x2+(y-
(t为参数) ,圆的直角坐标方程为x2+(y-![]() )2=5.
)2=5.
(Ⅱ)联立直线与圆的方程,利用t的几何意义可得|PA||PB|=|t1t2|=4.
(2)(Ⅰ)将函数零点分段可得函数的最小值为1;
(Ⅱ)由题意结合均值不等式的结论可得![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ)直线l参数方程为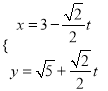 (t为参数)
(t为参数)
由ρ=2![]() sin θ,得x2+y2-2
sin θ,得x2+y2-2![]() y=0,
y=0,
即x2+(y-![]() )2=5.
)2=5.
(Ⅱ)将l的参数方程代入圆C的直角坐标方程,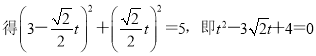
由于Δ=(-3![]() )2-4×4=2>0,故可设t1,t2是上述方程的两实根,
)2-4×4=2>0,故可设t1,t2是上述方程的两实根,
所以![]()
又直线l过点P(3,![]() ),
),
故由上式及t的几何意义|PA||PB|=|t1t2|=4
(2)解:(Ⅰ)由已知得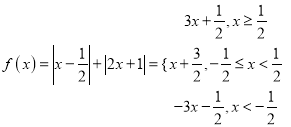 ,
,
可知函数![]() 的最小值
的最小值![]() 等于1.
等于1.
(Ⅱ)由(1)知![]() ,所以
,所以![]() 当且仅当
当且仅当![]() 时取等号.
时取等号.
即![]()
解得: ![]()

【题目】(本小题满分12分)某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据如表1所示
表1
参加社团活动 | 不参加社团活动 | 合计 | |
学习积极性高 | 17 | 8 | 25 |
学习积极性一般 | 5 | 20 | 25 |
合计 | 22 | 28 | 50 |
(1)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(2)运用独立检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
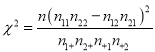
【题目】某土特产销售总公司为了解其经营状况,调查了其下属各分公司月销售额和利润,得到数据如下表:
分公司名称 | 雅雨 | 雅鱼 | 雅女 | 雅竹 | 雅茶 |
月销售额 | 3 | 5 | 6 | 7 | 9 |
月利润额 | 2 | 3 | 3 | 4 | 5 |
在统计中发现月销售额![]() 和月利润额
和月利润额![]() 具有线性相关关系.
具有线性相关关系.
(1)根据如下的参考公式与参考数据,求月利润额![]() 与月销售额
与月销售额![]() 之间的线性回归方程;
之间的线性回归方程;
(2)若该总公司还有一个分公司“雅果”月销售额为10万元,试估计它的月利润额是多少?
(参考公式: 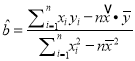 ,
, ![]() ,其中:
,其中: ![]() ,
, ![]() )
)